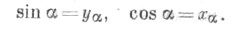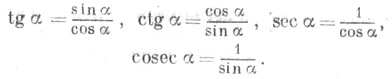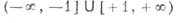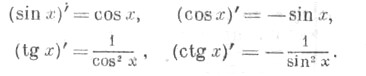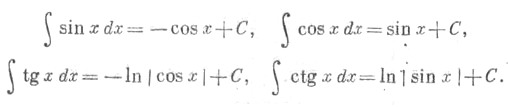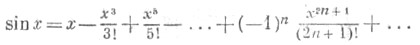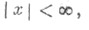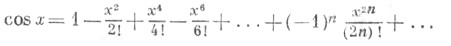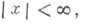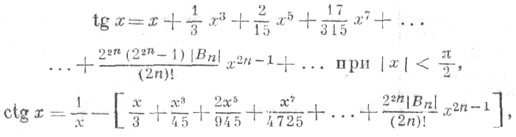что такое sec x в тригонометрии
СЕКАНС
Смотреть что такое «СЕКАНС» в других словарях:
СЕКАНС — (лат., от secare сечь, рассекать). В тригонометрии: радиус круга, проведенный из центра круга до конца касательной черты, за окружность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. СЕКАНС лат. secans, от secare … Словарь иностранных слов русского языка
СЕКАНС — (лат. secans секущая) одна из тригонометрических функций … Большой Энциклопедический словарь
СЕКАНС — [сэ], секанса, муж. (латин secans, букв. рассекающий) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношению гипотенузы к катету, прилежащему к углу. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
СЕКАНС — муж. тригоном. луч (радиус) круга, протянутый до конца касательной черты, за окружность. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
секанс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
секанс — секанс. Произносится [сэканс] … Словарь трудностей произношения и ударения в современном русском языке
Секанс — Рис. 1 Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса Тригонометрические функции вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x),… … Википедия
секанс — а; м. [от лат. secans секущий] Матем. Одна из тригонометрических функций угла, в прямоугольном треугольнике равная отношению гипотенузы к катету, прилежащему к данному углу. * * * секанс (лат. secans секущая), одна из тригонометрических функций … Энциклопедический словарь
Секанс — [лат. secans, здесь секущая (прямая); от seco режу, рассекаю], одна из тригонометрических функций (См. Тригонометрические функции); обозначение sec. В прямоугольном треугольнике С. острого угла называют отношение гипотенузы к катету,… … Большая советская энциклопедия
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
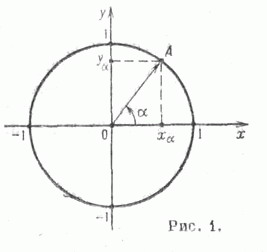
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Если 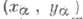
Остальные Т. ф. могут быть определены формулами
Все Т. ф.- периодические функции. Графики Т. ф. даны на рис. 2.
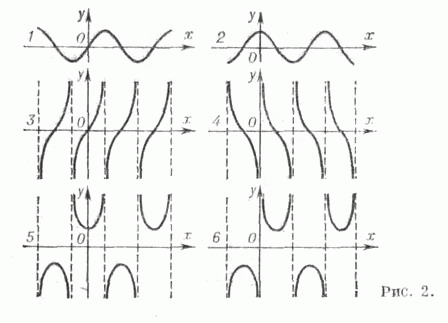
| 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | |
| sin α | 0 | 1 2 | 2 2 | 3 2 | 1 |
| cos α | 1 | 3 2 | 2 2 | 1 2 | 0 |
| tg α | 0 | 3 3 | 1 | 3 | нет |
| ctg α | нет | 3 | 1 | 3 3 | 0 |
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!