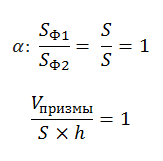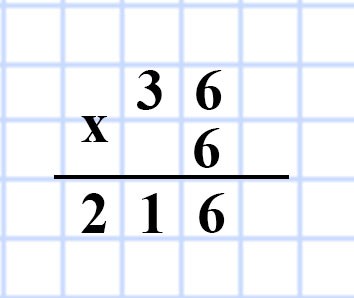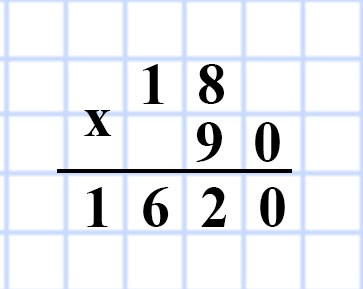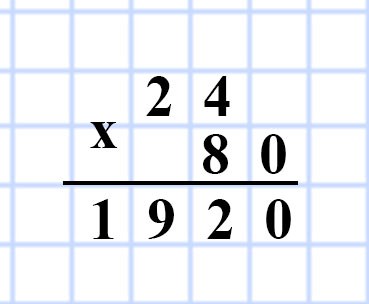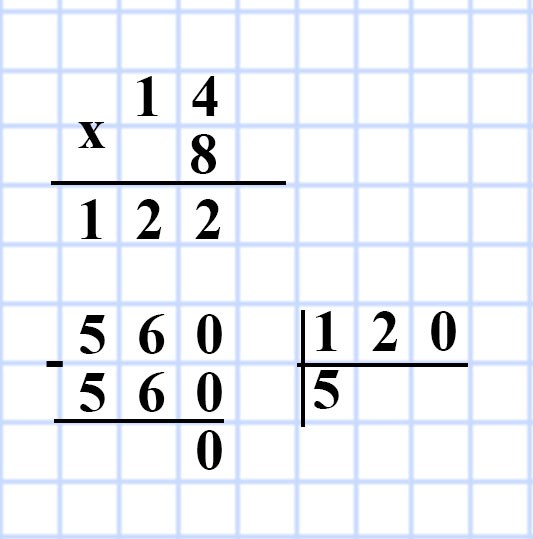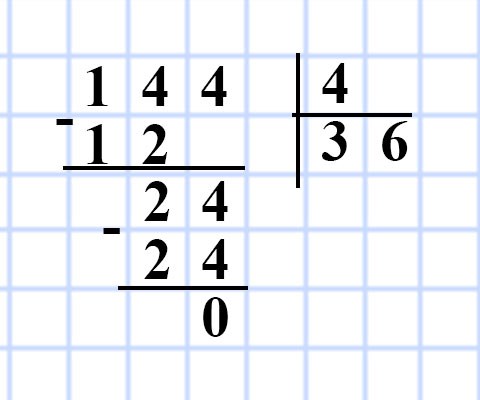что значит измерить объем фигуры
ВОПРОСЫ
1. Какими свойствами обладает объем фигуры?
1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.
2. Какой куб называют единичным?
3. Приведите примеры единиц измерения объема.
4. Что означает измерить объем фигуры?
5. Чему равен объем прямоугольного параллелепипеда с измерениями а, b, c?
6. По какой формуле вычисляется объем куба?
7. Как вычислить объем прямоугольного параллелепипеда, зная его площадь основания и высоту?
РЕШАЕМ УСТНО
1. Заполните пропуски в цепочки вычислений:
2. Сколько необходимо использовать кубиков с ребром 1 см, сложить кубик с ребром 2 см?
Нужно взять 8 кубиков с ребром 1 см.
3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?
УПРАЖНЕНИЯ
617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?
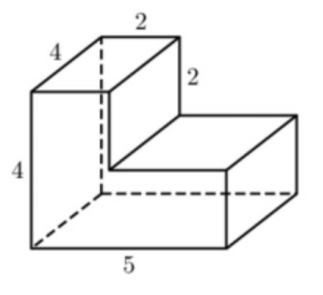
618. Фигуры, изображенные на рисунке 179, сложены из кубиков, ребра которых равны 1 см. Найдите объем каждой фигуры.
619. Вычислите объем прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.
620. Чему равен объем куба, ребро которого равно 6 см?
621. Чему равен объем прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?
622. Выразите:
1) в кубических миллиметрах: 7 см3, 38 см3; 12 см3 243 мм3; 42 см3 68 мм3; 54 см3 4 мм3; 1 дм3 20 мм3; 18 дм3 172 см3; 35 дм3 67 см3 96 мм3;
2) в кубических дециметрах: 4 м3; 264 м3; 10 м3 857 дм3; 28 м3 2 дм3; 44 000 см3; 5 430 000 см3.
623. Выразите в кубических сантиметрах: 8 дм3; 62 дм3; 378 000 мм3; 520 000 мм3; 78 дм3 325 см3; 56 дм3 14 см3; 8 м3 4 дм3 6 см3.
625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объем данного параллелепипеда.
629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объем равен 960 м3, а площадь пола равна 192 м2. Найдите высоту спортивного зала.
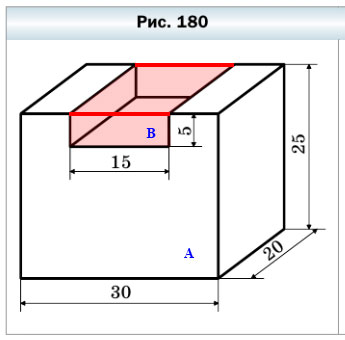
630. Найдите объем фигуры, изображенной на рисунке 180 (размеры даны в сантиметрах).
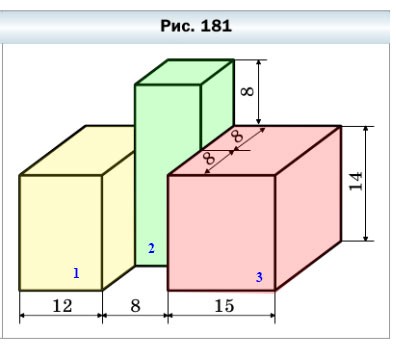
631. Найдите объем фигуры, изображенной на рисунке 181 (размеры даны в сантиметрах).
632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если 1 см3 цинка составляет 7 г.
633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм3 земли?
634. Куб и прямоугольный параллелепипед имеют равные объемы. Найдите площади поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.
635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объем первого куба больше объема второго?
638. В бассейн, площадь которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?
639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объем оставшейся части.
640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
642. Из двух населенных пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?
643. Найдите значение выражения:
ЗАДАЧА ОТ МУДРОЙ СОВЫ
Объемы геометрических тел
Объемы геометрических тел
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
Определение объема
Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:
Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.
В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.
Примеры
Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
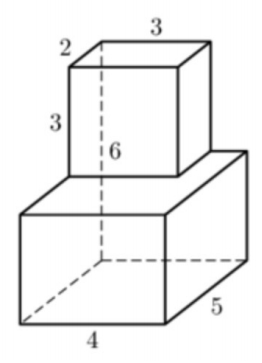
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Разберем, как можно вычислять объемы изучаемых в школе фигур.
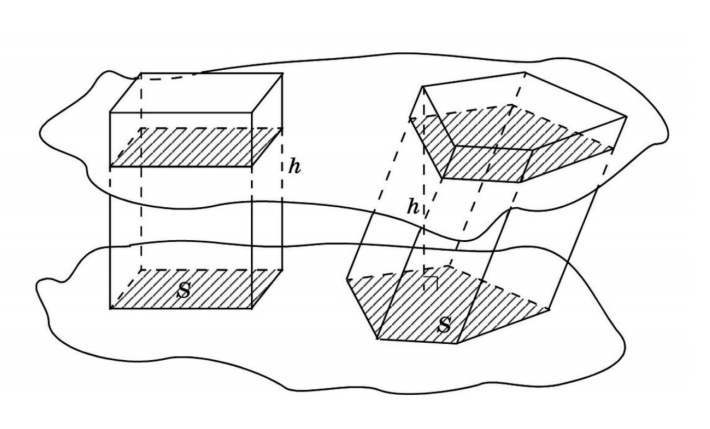
Объем призмы
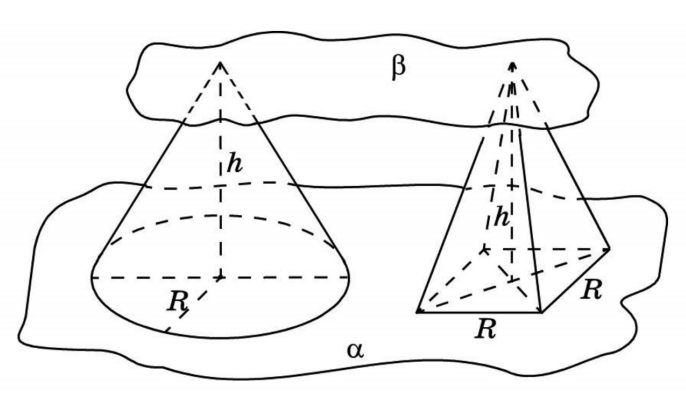
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф2) поместим прямоугольный параллелепипед (Ф1), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:
Объем пирамиды
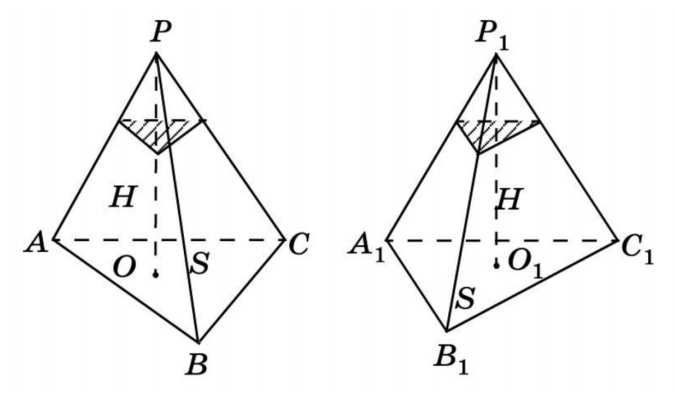
Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.
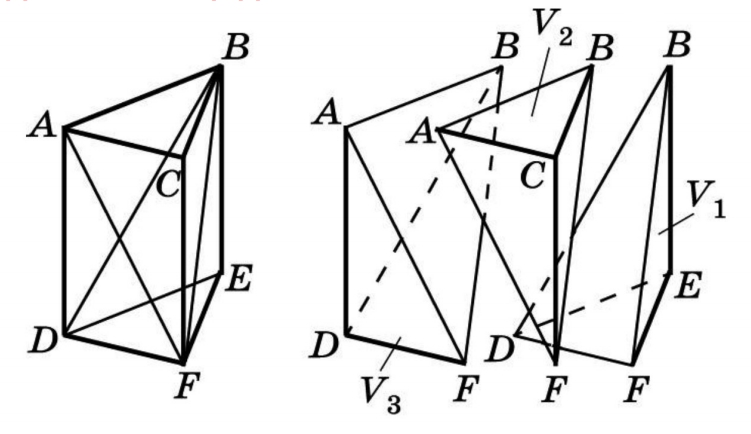
Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:
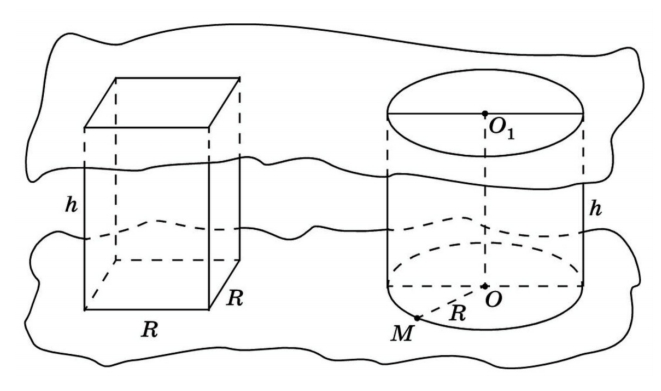
Объем цилиндра
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:
Объем конуса
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.
Объем шара
Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.
Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.
Мерзляк 5 класс — § 23. Объём прямоугольного параллелепипеда
Вопросы к параграфу
1. Какими свойствами обладает объём фигуры?
2. Какой куб называют единичным?
Единичным называют куб, ребро которого равно единичному отрезку.
3. Приведите примеры единиц измерения объёма.
4. Что означает измерить объём фигуры?
Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается.
5. Чему равен объём прямоугольного параллелепипеда с измерениями а, b, с?
V = abc
6. По какой формуле вычисляют объём куба?
7. Как вычислить объём прямоугольного параллелепипеда, зная его площадь основания и высоту?
V = Sh
Решаем устно
1. Заполните пропуски в цепочке вычислений:
2. Сколько необходимо использовать кубиков с ребром 1 см, чтобы сложить кубик с ребром 2 см?
Чтобы сложить кубик с ребром 2 см, надо использовать 8 кубиков с ребром 1 см.
3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?
3 • 4 + 5 • 4 + 6 • 4 = 12 + 20 + 24 = 56 (см) — проволоки.
4. Расставьте вместо звёздочек знаки «+» и «—» так, чтобы запись 20 * 30 * 10 * 80 * 70 = 50 стала верным равенством.
20 + 30 — 10 + 80 — 70 = (20 + 30) + (80 — 10 — 70) = 50 + 0 = 50
Упражнения
617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?
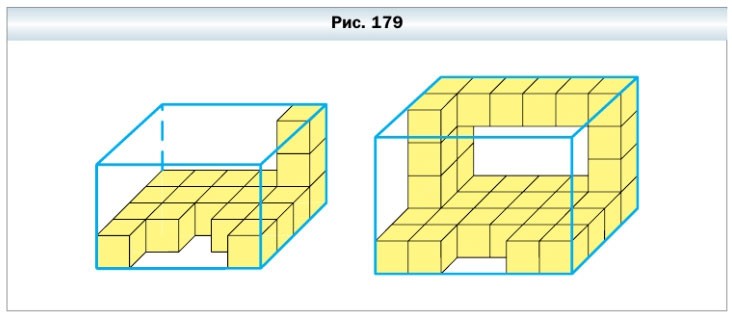
618. Фигуры, изображённые на рисунке 179, сложены из кубиков, рёбра которых равны 1 см. Найдите объём каждой фигуры.
Для того, чтобы найти объём фигуры, надо посчитать количество единичных кубов, из которых она состоит.
1 фигура (на рисунке слева):
V = 5 • 2 + 3 + 3 + 2 = 10 + 8 = 18 см³
2 фигура (на рисунке справа):
V = 6 • 3 + 2 +2 + 3 • 2 + 5 + 2 = 18 + 4 + 6 + 7 = 18 + 17 = 35 см³
Ответ: 18 см³ и 35 см³.
619. Вычислите объём прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.
Дано:
Решение:
V = abc = 12 • 15 • 6 = 12 • 90 = 1 080 м³
620. Чему равен объём куба, ребро которого равно 6 см?
Дано:
Решение:
V= a³ = 6³ = 36 • 6 = 216 см³
621. Чему равен объём прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?
Дано:
Решение:
V = abc = 10 • 8 • 4 = 10 • 32 = 320 дм³
622. Выразите:
1) в кубических миллиметрах:
12 см³ 243 мм³ = 12 000 мм³ + 243 мм³ = 12 243 мм³
42 см³ 68 мм³ = 42 000 мм³ + 68 мм³ = 42 068 мм³
54 см³ 4 мм³; = 54 000 мм³ + 4 мм³ = 54 004 мм³
1 дм³ 20 мм³ = 1 000 000 мм³ + 20 мм³ = 1 000 020 мм³
18 дм³ 172 см³ = 18 000 000 мм³ + 172 000 мм³ = 18 172 000 мм³
35 дм³ 67 см³ 96 мм³ = 35 000 000 мм³ + 67 000 мм³ + 96 мм³ = 35 067 096 мм³
2) в кубических дециметрах:
10 м³ 857 дм³ = 10 000 дм³ + 857 дм³ = 10 857 дм³
28 м³ 2 дм³ = 28 000 дм³ + 2 дм³ = 28 002 дм³
5 430 000 см³ = 5 430 дм³
623. Выразите в кубических сантиметрах:
378 000 мм³ = 378 см³
520 000 мм³ = 520 см³
78 дм³ 325 см³ = 78 000 см³ + 325 см³ = 78 325 см³
56 дм³ 14 см³ = 56 000 см³ + 14 см³ = 56 014 см³
8 м³ 4 дм³ 6 см³ = 8 000 000 см³ + 4 000 см³ + 6 см³ = 8 004 006 см³
624. Ширина прямоугольного параллелепипеда равна 15 дм, длина — на 3 дм больше ширины, а высота — в 3 раза меньше длины. Найдите объём данного параллелепипеда.
Дано:
Решение:
1) 15 + 3 = 18 (дм) — длина прямоугольного параллелепипеда.
2) 18 : 3 = 6 (дм) — высота прямоугольного параллелепипеда.
3) 18 • 15 • 6 = 18 • 90 = 1 620 (дм³) — объем V прямоугольного параллелепипеда.
625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объём данного параллелепипеда.
Дано:
Решение:
1) 20 + 4 = 24 (см) — длина прямоугольного параллелепипеда.
2) 20 : 5 = 4 (см) — ширина прямоугольного параллелепипеда.
3) 24 • 5 • 20 = 24 • 80 = 1 920 (дм³) — объем V прямоугольного параллелепипеда.
626. Объём прямоугольного параллелепипеда равен 560 см³, длина — 14 см, ширина — 8 см. Найдите высоту данного параллелепипеда.
Дано:
Решение:
V = Sh, значит h = V : S
1) 14 • 8 = 122 (см²) — площадь основания S прямоугольного параллелепипеда.
2) 560 : 120 = 5 (см) — высота h прямоугольного параллелепипеда.
627. Длина прямоугольного параллелепипеда равна 18 см, высота — 15 см, а объём — 3 240 см³. Найдите ширину данного параллелепипеда.
Дано:
Решение:
V = Sh, значит S = V : h
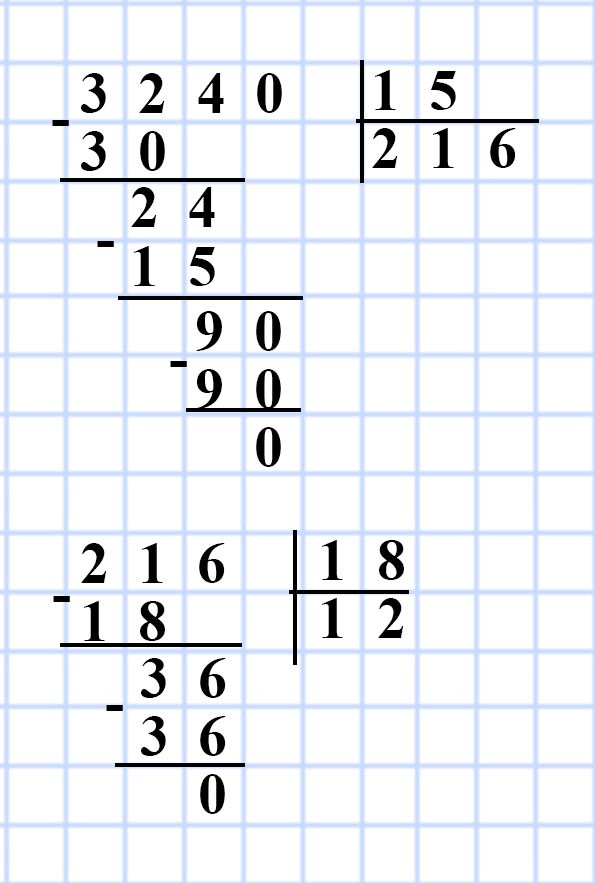
1) 3 240 : 15 = 216 (см²) — площадь основания S прямоугольного параллелепипеда.
S = a • b, значит b = S : a
2) 216 : 18 = 12 (см) — ширина b прямоугольного параллелепипеда.
628. Объём комнаты, имеющей форму прямоугольного параллелепипеда, равен 144 м³, а высота — 4 м. Найдите площадь пола комнаты.
Дано:
Решение:
V = Sh, значит S = V : h
1) 144 : 4 = 36 (м²) — площадь пола комнаты.
629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объём равен 960 м³, а площадь пола равна 192 м². Найдите высоту спортивного зала.
Дано:
Решение:
V = Sh, значит h = V : S
1) 960 : 192 = 5 (м) — высота спортивного зала.
630. Найдите объём фигуры, изображённой на рисунке 180 (размеры даны в сантиметрах).
Выполним дополнительное построение: проведём линии, соединяющие выступающие части исходной фигуры. Теперь можно сказать, что V = VА— VВ, где:
VА = 30 • 20 • 25 = 600 • 25 = 15 000 (cм³)
VА = 15 • 5 • 20 = 15 • 100 = 1 500 (cм³)
V = VА— VВ = 15 000 — 1 500 = 13 500 (cм³)
631. Найдите объём фигуры, изображённой на рисунке 181 (размеры даны в сантиметрах).
Фигуру, изображенную на рисунке 181, можно разделить на три прямоугольных параллелепипеда:
Рассмотрим прямоугольный параллелепипед № 3 (красный):
V3 = 15 • 16 • 14 = 240 • 14 = 3 360 (cм³)
Рассмотрим прямоугольный параллелепипед № 2 (зелёный):
V2 = 8 • 8 • 22 = 64 • 22 = 1 408 (cм³)
Рассмотрим прямоугольный параллелепипед № 1 (жёлтый):
V1 = 12 • 16 • 14 = 192 • 14 = 2 688 (cм³)
Объем фигуры равен сумме объемов фигур, из которых она состоит.
V = V1 + V2 + V3= 2 688 + 1 408 + 3 360 = 7 456 (cм³)
632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если масса 1 см³ цинка составляет 7 г.
Дано:
Решение:
V = 4 • 4 • 4 = 16 • 4 = 64 (см³)
Масса 1 см³ куба равна 7 г, значит масса 64 см³ равна:
633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм³ земли?
1) 15 000 • 80 • 60 = 1 200 000 • 60 = 72 000 000 (см³) — объем выкопанной машиной траншеи.
72 000 000 см³ = 72 м³
2) 72 : 8 = 9 (м³) — выкапывает машина за 1 час.
3) 72 000 : 240 = 300 (человек) — коротышек могут заменить 1 машину.
Ответ: 9 м³, 300 коротышек.
634. Куб и прямоугольный параллелепипед имеют равные объёмы. Найдите площадь поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.
1) 12 • 2 = 6 (см) — сторона b прямоугольного параллелепипеда.
2) 12 • 4 = 3 (см) — сторона с прямоугольного параллелепипеда.
3) V = a • b • c = 12 • 6 • 3 = 72 • 3 = 216 (см³) — объём прямоугольного параллелепипеда.
V (прямоугольного параллелепипеда) = V (куба) = a³ = 216 (см³)
Значит сторона куба равна такому числу, которое при возведении в третью степень равно 216. Методом подбора можем определить что это число 6, то есть сторона квадрата а = 6 см.
У куба 6 одинаковых граней, площадь каждой из которых равна а².
4) а² = 6 • 6 = 36 (см²) — площадь поверхности одной грани куба.
5) 36 • 6 = 216 (см²) — площадь поверхности куба.
Ответ: Площадь поверхности куба равна 216 см².
635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объём первого куба больше объёма второго?
Пусть длина ребра второго куба равна х единиц, тогда длина ребра первого куба будет равна 4х единиц.
S2 = 6a² = 6x² (ед²) — площадь поверхности второго куба.
S1 = 6a² = 6(4x)² = 6 • (4 • 4 • x • x) = 6 • 16 x² = 96 x² (ед²) — площадь поверхности первого куба.
S2 : S1 =96 x² : 6x² = 96 : 6 = 16 (раз) — площадь поверхности первого куба больше площади поверхности второго куба.
V2 = a³ = х³ (ед³) — объём второго куба.
V1 = a³ = (4х)³ = 4 • 4 • 4 • x • x • x = 16 • 4 • х³ = 64 х³ (ед³) — объём второго куба.
V1 : V2= 64 х³ : х³ = 64 (раза) — объём первого куба больше объёма второго куба.
Ответ: Площадь поверхности больше в 16 раз, объём больше в 64 раза.
636. Как изменится объём прямоугольного параллелепипеда, если:
1) длину увеличить в 4 раза, ширину — в 2 раза, высоту — в 5 раз
V1 = (4 • a) • (2 • b) • (5 • c) = (4 • 2 • 5) abc = 40 abc
V1 : V = 40 abc : abc = 40 (раз)
Ответ: объём увеличится в 40 раз.
2) ширину уменьшить в 4 раза, высоту — в 2 раза, а длину увеличить в 16 раз
V1 = (16 • a) • (b : 4) • (c : 2) = (16 : 4 : 2) abc = (4 : 2) abc = 2 abc
V1 : V = 2 abc : abc = 2 (раза)
Ответ: объём увеличится в 2 раза.
637. Как изменится объём прямоугольного параллелепипеда, если:
1) каждое измерение увеличить в 2 раза
V1 = (2 • a) • (2 • b) • (2• c) = (2 • 2 • 2) abc = 8 abc
V1 : V = 8 abc : abc = 8 (раз)
Ответ: объём увеличится в 8 раз.
2) длину уменьшить в 3 раза, высоту — в 5 раз, а ширину увеличить в 15 раз
V1 = (a : 3) • (b • 15) • (c : 5) = (15 : 3 : 5) abc = (5 : 5) abc = abc
V1 : V = abc : abc = 1 (раз)
Ответ: объём не изменится.
638. В бассейн, площадь дна которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?
S = 1 га = 10 000 м² = 1 000 000 дм²
V = 1 000 000 л = 1 000 000 дм³
V = S • h, значит h = V : S
h = V : S = 1 000 000 дм³ : 1 000 000 дм² = 1 дм = 10 см — высота налитой в басейн воды.
Это значит, что плавать в этом бассейне невозможно.
Ответ: Нет, соревнования по плаванию провести нельзя.
639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объём оставшейся части.
1) V (куба) = a³ = 3³ = 9 • 3 = 27 (см³) — объём куба с ребром 3 см.
2) V (одного отверстия) = abc = 1 • 1 • 3 = 3 (см³) — объем одного сквозного отверстия со стороной 1 см.
Так как все три отверстия пересекаются в центре куба, то объём вырезанной части:
3) V (вырезанной части) = 3 см³ • 3 ( размер трёх сквозных отверстий) — 1 см³ (размер пересечения второго отверстия в первым и третьим) — 1 см³ размер пересечения третьего отверстия с первым и вторым) = 9 — 1 — 1 = 7 (см³) — объём вырезанной части.
4) V (оставшейся части) = V (куба) — V (вырезанной части) = 27 — 7 = 20 (см³) — объём оставшейся части.
640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?
1) 12 • 6 • 4 = 72 • 4 = 288 (см³) — объём нового куска мыла.
2) (12 : 2) • (6 : 2) • (4 : 2) = 6 • 3 • 2 = 18 • 2 = 36 (см³) — объём мыла через 14 дней использования.
3) 288 — 36 = 252 ( см³) — мыла было использовано за 14 дней.
4) 252 : 14 = 18 (см³) — мыла используется за 1 день.
5) 36 : 18 = 2 (дня) — хватит оставшегося мыла.
Упражнения для повторения
641. В школьном коридоре, длина которого равна 30 м, ширина — 35 дм, надо заменить линолеум. Какое наименьшее количество рулонов линолеума для этого нужно, если длина рулона линолеума равна 12 м, а ширина — 160 см?
1) 350 = 2 • 160 + 30 (см)
Значит, для того, чтобы покрыть линолеумом в один ряд пол по ширине коридора необходимо использовать 2 рулона материала и ещё полосу шириной в 30 см.
Значит, для того, чтобы покрыть линолеумом в один ряд пол по длине коридора необходимо использовать 2 целых рулона и ещё одну половину рулона (6 = 12 : 2).
Половина рулона + половина рулона = 1 целый рулон.
Полосы 12 м х 30 см, 12 м х 30 см и 6 м х 30 см можно выкроить из 1 целого рулона.
Значит нам потребуется:
3) 2 + 2 + 1 + 1 = 6 (шт) — рулонов линолеума потребуется для замены линолеума в школьном коридоре.
642. Из двух населённых пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?
1) 12 • 2 = 24 (км) — проехал первый велосипедист до места встречи.
2) 54 — 24 = 30 (км) — проехал второй велосипедист до места встречи.
3) 30 : 2 = 15 (км/ч) — скорость второго велосипедиста.
643. Найдите значение выражения:
1) 7a + 7b, если a + b = 14
7a + 7b = 7 (a + b) = 7 • 14 = 98
2) m • 17 + n • 17, если m + n = 1 000
m • 17 + n • 17 = 17 (m + n) = 17 • 1 000 = 17 000
3) k • 9 + 9l, если k + l = 12
k • 9 + 9l = 9 (k + l) = 9 • 12 = 108
4) 4c — 4d, если с — d = 125
4c — 4d = 4 (c — d) = 4 • 125 = 500
5) x • 23 — 23y, если x — у = 4
x • 23 — 23y = 23 (x — y) = 23 • 4 = 92
6) 56p — r • 56, если р — r = 11
56p — r • 56 = 56 (p — r) = 56 • 11 = 616
Задача от мудрой совы
644. В записи первого трёхзначного числа используются только цифры 2 и 3, а в записи второго — только цифры 3 и 4. Может ли произведение этих чисел записываться только цифрами 2 и 4?
Если в записи первого трёхзначного числа используются только цифры 2 и 3, то таким трёхзначным числом могут быть числа:
Если в записи второго трёхзначного числа используются только цифры 3 и 4, то таким трёхзначным числом могут быть числа:
Расположим их в виде таблицы:
Мы видим, что ни одно произведение не удовлетворяет условию. Значит записать такое произведения только цифрами 2 и 4 невозможно.