что значит канонический вид уравнения

Каноническое уравнение прямой на плоскости: теория, примеры, решение задач

Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.

Понятие канонического уравнения прямой

Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:

Если преобразовать полученное равенство в координатную форму, то мы получим:

Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:

Разберем важный пример задачи на нахождение канонического уравнения.

Решение

Получившееся в итоге равенство и будет нужным ответом.

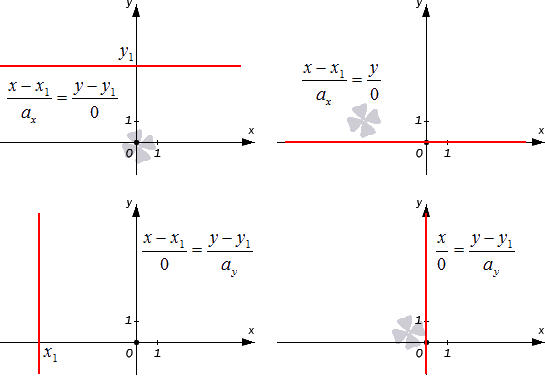
Проиллюстрируем два частных случая канонического уравнения, описанные выше:

Решение

На рисунке изображена прямая. Запишите ее каноническое уравнение.

Решение

Преобразование канонического уравнения прямой в другие виды уравнений

Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.

Покажем на примере, как именно выполняется это действие с конкретными числами.

Решение

Далее можно перейти к формулированию необходимых параметрических уравнений:

Решение

Делаем указанные выше действия по порядку.

Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.

Решение

Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.

Далее переходим к формулировке уравнения прямой в отрезках.

У нас получилось нужное нам каноническое уравнение прямой на плоскости.

Решение

Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.

Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x = x 1 + a x · λ y = y 1 + a y · λ и приравнять обе части равенств. Схема решения выглядит так:

Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.

Решение

Как решать задачи на составление канонических уравнений

В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.

Решение

Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.

Точно так же поступим и с координатами второй точки:

Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.

Ответ: первая точка лежит на заданной прямой, а вторая нет.

Решение

Равенство верное, значит, эта точка расположена на заданной прямой.

Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.

Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.

Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.

Решение

Ответ: x 2 = y + 3 1

Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.

Решение

Решение

Источник

Что такое канонический вид уравнения?

Понятие алгебраической линии и её порядка

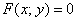
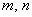
Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид , где – многочлен, состоящий из слагаемых вида ( – действительное число, – целые неотрицательные числа).

Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательных степенях.

Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости

Порядок линии равен максимальному значению 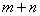входящих в него слагаемых.

По соответствующей теореме, понятие алгебраической линии, а также её порядок не зависят от выбора аффинной системы координат, поэтому для лёгкости бытия считаем, что все последующие выкладки имеют место быть в декартовых координатах .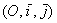

Общее уравнение линии второго порядка имеет вид , где – произвольные действительные числа ( принято записывать с множителем-«двойкой»), причём коэффициенты не равны одновременно нулю.

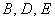
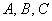
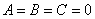
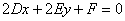
Если , то уравнение упрощается до , и если коэффициенты одновременно не равны нулю, то это в точности общее уравнение «плоской» прямой, которая представляет собой линию первого порядка.

Многие поняли смысл новых терминов, но, тем не менее, в целях 100%-го усвоения материала сунем пальцы в розетку. Чтобы определить порядок линии, нужно перебрать все слагаемые её уравнения и у каждого из них найти сумму степеней входящих переменных.

слагаемое 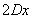содержит «и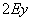кс» в 1-й степени;
слагаемое содержит «игрек» в 1-й степени;
в слагаемом 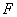переменные отсутствуют, поэтому сумма их степеней равна нулю.

Далее из полученных чисел выбирается максимальное значение, в данном случае единица, – это и есть порядок линии.

Теперь разберёмся, почему уравнение 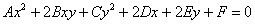задаёт линию второго порядка:

слагаемое содержит «икс» во 2-й степени;
у слагаемого сумма степ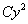еней переменных: 1 + 1 = 2;
слагаемое содержит «игрек» во 2-й степени;
все остальные слагаемые – меньшей степени.

Максимальное значение: 2

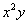
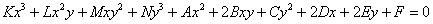
Если к нашему уравнению дополнительно приплюсовать, скажем, , то оно уже будет определять линию третьего порядка. Очевидно, что общий вид уравнения линии 3-го порядка содержит «полный комплект» слагаемых, сумма степеней переменных в которых равна трём:
, где коэффициенты не равны одновременно нулю.

В том случае, если добавить одно или несколько подходящих слагаемых, которые содержат 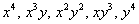, то речь уже зайдёт о линии 4-го порядка, и т.д.

С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат.

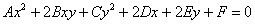
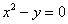
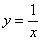
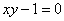
Однако вернёмся к общему уравнению и вспомним его простейшие школьные вариации. В качестве примеров напрашивается парабола , уравнение которой легко привести к общему виду , и гипербола с эквивалентным уравнением . Однако не всё так гладко….

Существенный недостаток общего уравнения состоит в том, что почти всегда не понятно, какую линию оно задаёт. Даже в простейшем случае 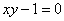не сразу сообразишь, что это гипербола. Такие расклады хороши только на маскараде, поэтому в курсе аналитической геометрии рассматривается типовая задача приведения уравнения линии 2-го порядка к каноническому виду.

Что такое канонический вид уравнения?

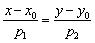
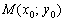
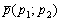
Это общепринятый стандартный вид уравнения, когда в считанные секунды становится ясно, какой геометрический объект оно определяет. Кроме того, канонический вид очень удобен для решения многих практических заданий. Так, например, по каноническому уравнению «плоской» прямой, во-первых, сразу понятно, что это прямая, а во-вторых – элементарно просматривается принадлежащая ей точка и направляющий вектор .

Очевидно, что любая линия 1-го порядка представляет собой прямую. На втором же этаже нас ждёт уже не вахтёр, а гораздо более разнообразная компания из девяти статуй:

Дата добавления: 2021-01-20 ; просмотров: 24 ; Мы поможем в написании вашей работы!

Источник

Кривые второго порядка. Канонический вид уравнений второго порядка.

Кривая второго порядка — геометрическое место точек на плоскости, прямоугольные координаты

которых удовлетворяют уравнению вида:

в котором, по крайней мере один из коэффициентов a₁₁, a₁₂, a₂₂ не равен нулю.

Инварианты кривых второго порядка.

Вид кривой зависим от 4 инвариантов, приведенных ниже:

— инварианты относительно поворота и сдвига системы координат:

— инвариант относительно поворота системы координат (полуинвариант):

Для изучения кривых второго порядка рассматриваем произведение А*С.

Общее уравнение кривой второго порядка выглядит так:

Ax 2 +2Bxy+Cy 2 +2Dx+2Ey+F=0

— Если А*С > 0, то уравнение принимает вид уравнения эллиптического типа. Любое эллиптическое

уравнение – это уравнение или обычного эллипса, или же вырожденного эллипса (точки), или мнимого

эллипса (в таком случае уравнение не определяет на плоскости ни одного геометрического образа);

уравнение выражает или простую гиперболу, или вырожденную гиперболу (две пересекающиеся прямые);

— Если А*С = 0, то линия второго порядка не будет центральной. Уравнения такого типа называют

уравнениями параболического типа и выражают на плоскости или простую параболу, или 2 параллельных

(либо совпадающих) прямых, или не выражают на плоскости ни одного геометрического образа;

— Если А*С ≠ 0, кривая второго порядка будет центральной;

Таким образом, виды кривых второго порядка:

Канонический вид уравнений второго порядка.

Вводя новую систему координат можно привести уравнения кривых второго порядка к стандартному

каноническому виду. Характеристики канонических уравнений очень легко выражаются через инварианты

Δ, D, I и корни характеристического уравнения .

Источник

Каноническое уравнение прямой на плоскости

В данной статье мы рассмотрим каноническое уравнение прямой на плоскости. Определим понятие направляющего вектора прямой. Рассмотрим примеры построения канонического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим метод преобразования уравнения в каноническом виде в параметрический и общий виды.

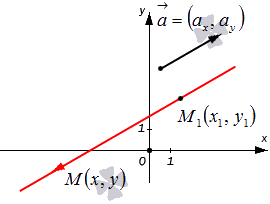
Определение 1. Любой ненулевой вектор, параллельный данной прямой называется направляющим вектором этой прямой.

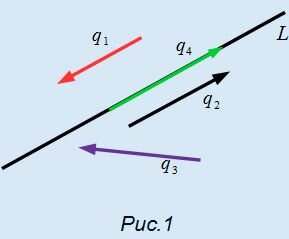На рисунке Рис.1 представлена прямая L и векторы q₁, q₂, q₃, q₄. Из определения следует, что векторы q₁, q₂, q₄ являются направляющими векторами прямой L, а q₃ − нет.

Каноническое уравнение прямой L на плоскости представляется следующей формулой:

где x₁, y₁ координаты некоторой точки M₁ на прямой L. Вектор q=<m, p> является направляющим вектором прямой L.

Надо отметить, что при записи уравнения прямой в каноническом виде, допускается, чтобы один из чисел m и p была равна нулю (одновременно m и p не могут быть равным нулю, т.к. направляющий вектор прямой не должен быть нулевым вектором). Равенство нулю одного из знаменателей означает равенство нулю соответствующего числителя. В этом можно убедится, записав уравнение (1) в следующем виде:

Выше мы отметили, что прямая L проходит через точку M₁(x₁, y₁). В этом можно убедится, подставив x=x₁, y=y₁ в уравнение (1).

Чтобы убедится, что точки M₁(x₁, y₁) и M₂(x₂, y₂) находятся на прямой L, поочередно подставим в уравнение (3) координаты точек M₁ и M₂. Получим тождества, следовательно эти точки принадлежат прямой L.

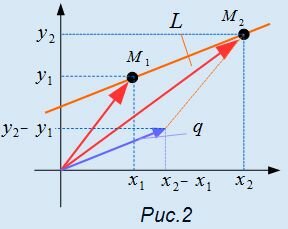Сравним уравнения (1) и (3). Тогда можно записать q=<m, p>=<x₂−x₁, y₂−y₁>. На рисунке Рис.2 представлен вектор q, которая является разностью векторов, соответствующих точкам M₂ и M₁. Этот вектор является направляющим вектором прямой L. Следовательно, для определения направляющего вектора прямой, достаточно взять две точки на данной прямой и найти разность между соответсвующими координатами этих точек.

Таким образом, прямая на плоскости определяется точкой и направляющим вектором или двумя точками.

Онлайн калькулятор, для построения прямой через две точки находится тут.

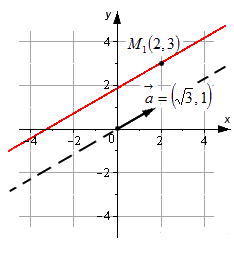
Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=<−3, 5>. Построить каноническое уравнение прямой.

Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

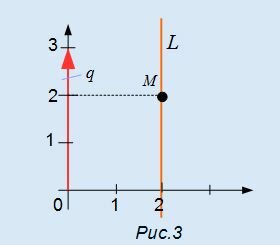
Пример 2. Прямая проходит через точку M=(2, 2) и имеет направляющий вектор q=<0, 3>. Построить каноническое уравнение прямой.

Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

На рисунке Рис.3 изображена прямая L, точка M=(2, 2) и направляющий вектор q=<0, 3>. Прямая проходит через точку M и параллельна направляющему вектору q.

Пример 3. Прямая проходит через точки M₁=(−7, 2) и M₂=(−4, 4). Построить каноническое уравнение прямой. Воспользуемся формулой (3). Подставим координаты точек в уравнение (3):

Упростим полученное уравнение:

Приведение канонического уравнения прямой на плоскости к параметрическому виду

Для приведения канонического уравнения прямой на плоскости к параметрическому виду, обозначим каждую часть уравнения (1) переменным t:

Выразим переменные x и y через t:

где t называется параметром, а уравнение (4) называется параметрическим уравнением прямой.

Для построения уравнения прямой, представленной параметрическом виде (4), достаточно задать параметру t любые значения и вычислить из уравнений (4) соответствующие координаты x и y некоторых точек. Затем провести через эти точки прямую.

Обратное преобразование смотрите здесь.

Пример 4. Каноническое уравнение прямой задана следующим уравнением:

Найти параметрическое уравнение прямой.

Решение. Обозначим через t левую и правую части уравнения (5):

Выразим переменные x и y через t:

Приведение канонического уравнения прямой на плоскости к общему виду

Пусть прямая на плоскости задана каноническим уравнением прямой (1). Преобразовав (1) получим:

Сделаем следующие обозначения:

Тогда уравнение (6) можно записать в следующем виде:

где n=<A,B> − называется нормальным вектором прямой.

Нетрудно заметить, что нормальный и направляющий векторы прямой перепендикулярны, т.е. скалярное произведение этих векторов равно нулю:

Обратное преобразование смотрите здесь.

Пример 5. Каноническое уравнение прямой задана следующим уравнением:

Записать общее уравнение прямой.

Решение. Сделаем преобразования уравнения (7):

Источник

Каноническое уравнение прямой в пространстве

Вы будете перенаправлены на Автор24

Существует несколько различных типов уравнений, описывающих кривую первого порядка, называемую прямой. Каждый из них оптимален для какой-то своей цели. Давайте познакомимся с ними поближе.

Каноническое уравнение прямой в пространстве

Канонический вид уравнения прямой в пространстве выглядит как следующее равенство:

Не во всех случаях удобно и практично пользоваться каноническим уравнением, поэтому частенько возникает надобность использовать какое-то другое, например, можно прибегнуть к параметрическому.

Для каких прямых не представляется возможным или нельзя написать каноническое уравнение?

Глядя на это уравнение, видно, что его возможно использовать только в том случае, если координаты направляющих векторов исследуемых прямых не равны нулю, для таких прямых стоит воспользоваться параметрическими уравнениями.

Параметрический вид уравнений прямой в пространстве такой:

$\begin x = x_1 + α \cdot λ \\ y = y_1 + β \cdot λ \\ z = z_1 + γ \cdot λ \\ \end$,

Параметрическое уравнение как раз удобно применять если одна из координат направляющего вектора равна нулю.

Чтобы произвести переход от параметрического вида уравнения к каноническому виду уравнения прямой в пространстве, осуществите вывод канонического уравнения прямой из параметрического.

Готовые работы на аналогичную тему

Уравнение прямой, образуемой пересечением двух плоскостей

Рисунок 1. Связь канонического и общего уравнения прямой

Для того чтобы составить каноническое уравнение прямой в пространстве, заданной пересечением плоскостей, необходимо познакомиться поближе с 2 исследуемыми плоскостями.

Любую плоскость, находящуюся в пространстве, можно описать с помощью равенства:

Соответственно, не нужно быть гением, чтобы понять, что если две плоскости пересечены между собой, то на их общей части будет возлежать некая прямая. Чтобы её найти, нужно получить общее решение следующей системы уравнений:

$\begin A_1x + B_1y + C_1z + D_1 = 0 \\ A_2x + B_2y + C_2z + D_2 = 0 \\ \end$

С помощью же частного решения этой системы уравнений можно узнать, принадлежит ли какая-либо точка трёхмерной системы координат описанным уравнениями плоскостям и, конечно же, нашей прямой. Для этого нужно просто подставить её икс, игрек и зет в систему.

Приведённая система уравнений является своеобразной “формулой”, служащей для нахождения общего уравнения прямой в пространстве.

Иногда в каких-либо практических задачах требуется получить из уравнения прямой в пространстве в общем виде параметрические или канонические уравнения, тогда в первую очередь вам стоит узнать координаты её направляющего вектора и какую-либо точку, находящуюся на изучаемой прямой.

Найдём нормальные вектора для плоскостей. Если кто забыл, нормальный вектор — это такой вектор, который является перпендикулярным (ортогональным) к данной плоскости или прямой.

Следующим этапом выполняем поиск координат точки, возлежащей на искомой прямой.

Составьте каноническое уравнение прямой, получаемой из системы уравнений, описывающей пару пересечённых плоскостей:

$\begin 2x – y + 3z + 4 = 0 \\ x + 5y – 3z – 7 = 0 \\ \end$

Найдём направляющий вектор, для этого сначала запишем вектора нормалей плоскостей:

Ну а сейчас пора вычислить сам направляющий вектор:

$\begin 2x + 3z + 4 = 0 \\ x – 3z – 7 = 0 \\ \end$

Подставим все полученные нами цифры и получим следующее уравнение:

Составление канонического уравнения прямой по координатам двух точек

Для того чтобы написать уравнение прямой в пространстве, проходящей через 2 точки, воспользуйтесь координатами ваших точек и внедрите их в следующее уравнение:

Это уравнение можно вывести из параметрического уравнения прямой.

Помещаем обнаруженные нами координаты вектора и точки в каноничное уравнение прямой в пространстве и получим уравнение прямой, проходящей через 2 точки.

Если же необходимо выразить именно параметрические уравнения из координат двух точек, через которые проведена некая одна прямая, то тут тоже всё довольно просто и без неожиданностей:

Источник