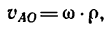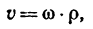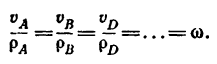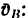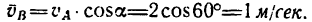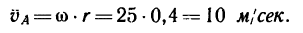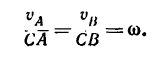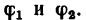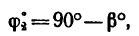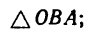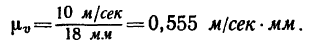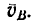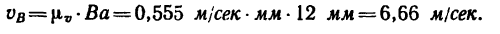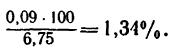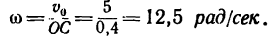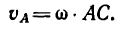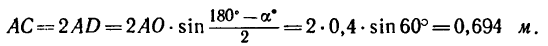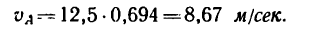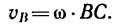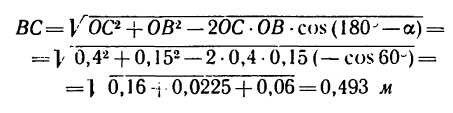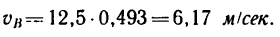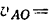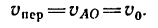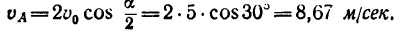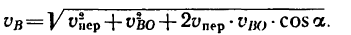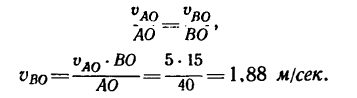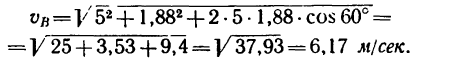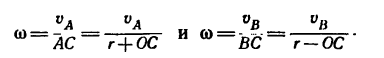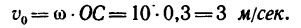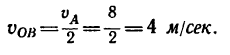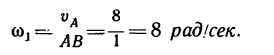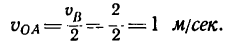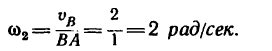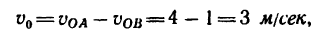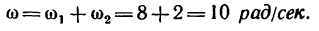что значит катится без скольжения

Качение без скольжения

Физика > Качение без скольжения

Качение без скольжения можно распределить на вращательное и поступательное движения.

Задача обучения

Основные пункты

Термины

Если с самого начала объект переворачивается без буксирования, то можно говорить о качении без проскальзывания. Чтобы разобраться, давайте рассмотрим пример с колесом на плоской горизонтальной поверхности.

Движение без проскальзывания понять намного проще, если выделить в нем движение центра масс с линейной скоростью v и вращательное движение вокруг центра с угловой скоростью w.

Движение качения отображает комбинацию вращательного и поступательного движений

Когда объект катится по плоскости без скольжения, точка контакта не смещается. Если представим, что колесо движется со скоростью v, то заметно, что оно должно также совершать движение вокруг своей оси с угловой скоростью ω.

Угловая скорость тела (ω) расположена прямо пропорционально скорости движения. Вы ведь могли заметить: чем быстрее разогналась машина, тем больше оборотов совершают колеса. Чтобы вычислить точную связь между линейной и угловой скоростями, можно взять случай, где колесо смещается на дистанцию х при повороте на углу θ.

Тело, скатывающееся на дистанцию х на плоскости, лишенной скольжения

В математике длина дуги приравнивается к углу сегмента, умноженному на радиус объекта (R). Отсюда выходит, что длина дуги колеса, повернутого на θ, достигает Rθ. Так как колесо постоянно контактирует с поверхностью, длина дуги также равна х. Выходит:

Не забывайте, что х и θ зависят от времени, поэтому возьмем их производные:

Здесь аналогичен v в линейной скорости, а – угловой скорости ω. Теперь можно все упростить:

Источник

Плоскопараллельное движение тела в теоретической механике

Плоскопараллельное движение тела:

Сложное плоскопараллельное движение твердого тела составляется из поступательного и вращательного движений. Это свойство является основой первого способа определения скорости любой точки тела, находящегося в плоскопараллельном движении.

1. Поступательная часть плоскопараллельного движения принимается за переносное и зависит от движения какой-либо произвольно выбранной точки, называемой полюсом. За полюс принимают всегда ту точку, скорость которой в данный момент известна.

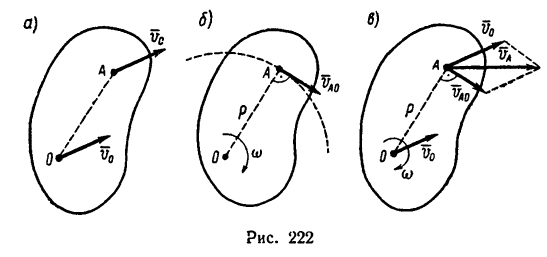
Если движение является только поступательным, то все точки тела, в том числе и точка А (рис. 222, а), имеют ту же скорость, что и полюс О.

2. Вращательная часть плоскопараллельного движения вокруг выбранного полюса принимается за относительное.

Если движение тела является только вращательным, то точка А совершает движение по окружности с центром в полюсе О со скоростью

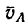
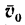
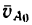
3. Абсолютная скорость точки А равна геометрической сумме переносной скорости полюса и ее относительной скорости вокруг полюса О (рис. 222, в). Таким образом, абсолютная скорость определяется либо при помощи правила параллелограмма, либо правила треугольника.

Второй способ определения скорости любой точки тела при его плоскопараллельным движении основан на использовании в качестве полюса мгновенного центра скоростей.

1. Как известно, мгновенным центром скоростей называется расположенная в плоскости сечения точка, абсолютная скорость которой в данный момент равняется нулю.

2. Если за полюс принять мгновенный центр скоростей, то в этот момент переносные (поступательные) скорости всех точек тела равны нулю и абсолютная скорость любой точки определяется по формуле

где —угловая скорость плоского сечения, которая не зависит от выбора полюса;

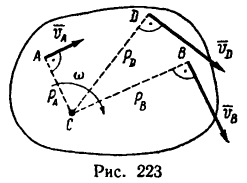
р—расстояние от мгновенного центра скоростей С до данной точки (рис. 223).

Для скоростей любых точек сечения имеем зависимость

При решении некоторых задач оказывается целесообразным использовать теорему о равенстве между собой проекций скоростей двух точек плоского сечения на прямую, соединяющую эти точки.

Задача №1

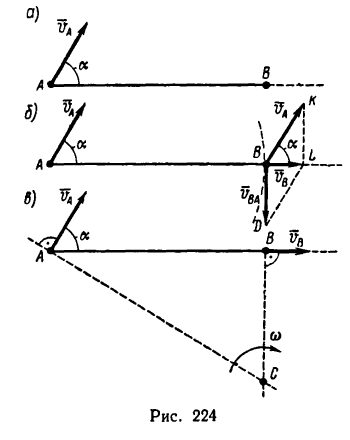
Стержень АВ двигается в плоскости чертежа. В момент, когда стержень занимает горизонтальное положение (рис. 224, а), скорость его точки А равна 2 м/сек и направлена под углом а=60° к прямой АВ. Определить скорость точки В, если известно, что она направлена вдоль АВ.

Решение 1—сложение переносной и относительной скоростей (рис. 224, б).

1. Примем за полюс точку А. Вместе с полюсом стержень АВ движется поступательно, поэтому точка В как слагаемая скорость имеет скорость полюса, т. е. 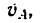которую изобразим у точки В вектором ВК

2. Вследствие вращения стержня вокруг полюса точка В имеет вторую слагаемую скорость 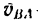— относительную скорость, направленную перпендикулярно к стержню.

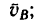
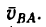
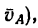
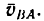
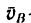
3. Построим параллелограмм скоростей. В параллелограмме известно направление диагонали, которая изобразит искомую скорость поэтому из точки К проведем до пересечения с продолжением АВ отрезок KL, параллельный направлению относительной скорости Затем из точки L проведем прямую LD, параллельную КВ (или вектору , до пересечения в точке D с линией, характеризующей направление Получается параллелограмм BKLD, в котором диагональ BL изображает —скорость точки В.

4. Находим числовое значение

BLK —прямоугольный (KL BL), поэтому

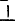
Решение 2 — при помощи мгновенного центра скоростей (рис. 224, в).

1. Из точек А и В проведем две прямые, перпендикулярные к направлениям скоростей Точка С пересечения этих прямых и определит положение мгновенного центра скоростей.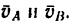

2. Вращение стержня АВ вокруг мгновенного центра скохарактеризуется угловой скоростью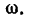
Поэтому
Отсюда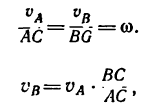

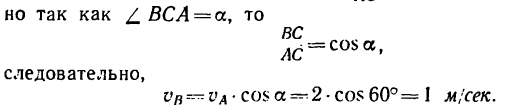
Решение 3—с применением теоремы о проекциях скоростей двух точек плоского сечения.

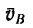
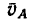
1. В рассматриваемом случае искомая скорость направлена вдоль прямой, соединяющей точки A и В; при этом известен угол между данной скоростью и той же прямой АВ. Поэтому удобно применить теорему: проекции скоростей двух точек плоского сечения на прямую, соединяющую эти точки, равны между собой.

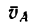
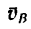
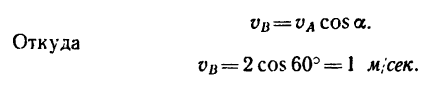
2. Спроектировав данную скорость и искомую на прямую АВ (см. рис. 224, в) и приравняв эти проекции, получим

При решении подобных задач иногда приходится выполнять довольно много промежуточных вычислений. Их можно избежать, если решить задачу графическим методом, но с приближенным результатом.

Поясним это на примере следующей задачи.

Задача №2

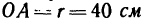
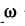
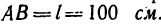
Кривошип кривошипно шатунного механизма (рис. 225, а) вращается с угловой скоростью= 25 рад/сек. Длина шатуна, приводящего ползун В в возвратно-поступательное движение вдоль горнтальных направляющих, равна Определить скорость ползуна В в тот момент, когда ОА образует с горнзонталью угол а = 30°.

Решение 1 — при помощи мгновенного центра скоростей (решение путем сложения переносной и относительной скоростей рекомендуется выполнить самостоятельно).

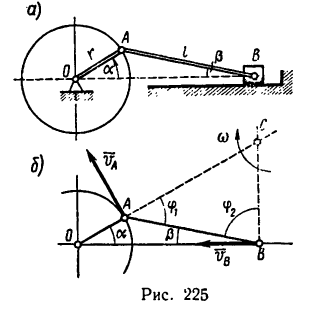
1. Изобразим на рис. 225, б расчетную схему. Схематично покажем кривошип ОА и шатун АВ в заданном положении. Ползун В, можно отождествить с точкой В.

2. Замечаем, что кривошип cobcj ползун В движется поступательно, ■ параллельное движение.

3. Скорость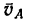точки А направлю шипу 0/1 (по касательной к окр точка А). Ее числовое значение

Скорость 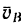точки В направлена

Проведем из точек А и В пря правлениям скоростей 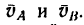Пай мгновенный центр скоростей шатунг

4. Найдя положение мгновенноп центра скоростей, получим = 0).

Отсюда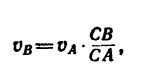

но предварительно нужно узнать значение отношения 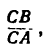которое,

как легко заметить, равно отношению синусов противолежащих углов (теорема синусов):

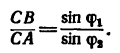
5. Чтобы определить величину этого отношения, необходимо определить углы

Замечая, что (см. рис. 225, б)

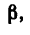
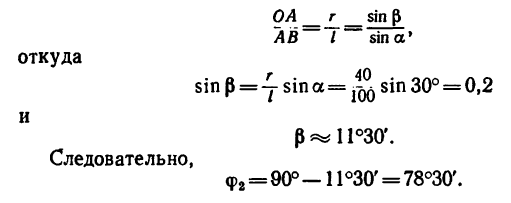
найдем угол применив теорему синусов к

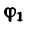
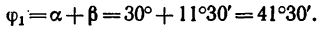
Из того же рис. 225, б видно, что угол является одним из внешних углов ОВА, поэтому

6. Теперь можно определить числовое значение скорости ползуна В:

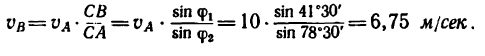
Решение 2—графическим методом.

1. Построим в масштабе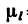=2,22 см/мм сх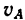ему кривошипношатунного механизма в заданном положении (рис. 226).

2. Скорость = 10 м/сек точки А изобразим отрезком АК =18 мм. Значит масштаб скоростей

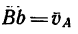
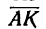
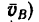
3. Из точки В построим вектор (вектор ВЬ равен вектору и параллелен отрезку АК)- Из точки b построим до пересечения с линией ВО (направлением скорости отрезок bа, перпендикулярный к- ВА. Получившийся на линии ВО вектор Ва изображает искомую скорость

4. Измерив длину отрезка Ва, найдем, что Ва — 12 мм. Следовательно, числовое значение скоростей точки В

5. Как видно, между результатом, вычисленным при помощи мгновенного центра скоростей (6,75), и результатом, найденным при графическом решении (6,66), имеется расхождение, равное

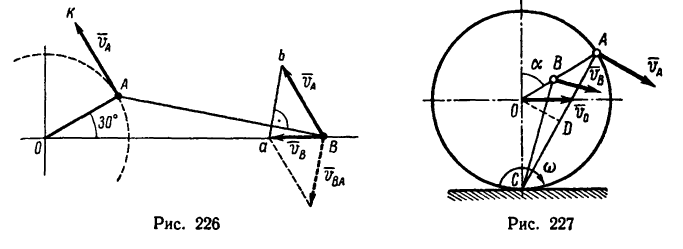
0,09 (абсолютная ошибка). Следовательно, относительная ошибка, допущенная в графическом решении, составляет

Задача №3

Колесо катится без скольжения по горизонтальной плоскости, причем ось колеса перемещается равномерно со скоростью 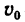= 5 м/сек. Определить абсолютную скорость точки А на ободе колеса и точки В, находящейся на том же радиусе, в момент, когда радиус колеса, равный ОА = г=40 см, образует с вертикалью угол а=60° (рис. 227). Расстояние ОВ = 15 см.

Решение 1—при помощи мгновенного центра скоростей.

1. Колесо катится без скольжения, следовательно, точка С соприкосновения колеса с горизонтальной плоскостью является мгновенным центром скоростей, так как абсолютная скорость этой точки ос=0 Если принять точку С за полюс, то можно считать, что в данный момент колесо совершает вращение вокруг так называемой мгновенной оси, перпендикулярной к плоскости колеса и проходящей через точку С (мгновенный центр скоростей).

2. Определяем угловую скорость колеса:

3. Определяем абсолютную скорость точки А. Скорость направлена перпендикулярно к прямой АС, соединяющей точку А с мгновенным центром скоростей С,

4. Определяем абсолютную скорость точки В. Скорость у0 направлена перпендикулярно к примой СВ и численно равна

Решение 2 —при помощи сложения переносной и относительной скоростей.

1. Катящееся колесо совершает сложное движение, складывающееся из поступательного движения колеса вместе с осью О (переносного движения) и вращения колеса вокруг оси О (относительного движения).

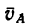
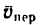
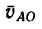
2. Абсолютная скорость точки А при таком рассмотрении движения колеса равна диагонали параллелограмма ACDE, построенного на переносной и относительной скоростях точки А (рис. 228).

3. Переносная скорость точки А равна скорости 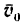колеса.

Найдем относительную скорость

точки А; Но угловая скорость относительного вращательного движения, как известно, не зависит от выбора полюса, поэтому, приняв за полюс

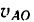
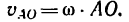
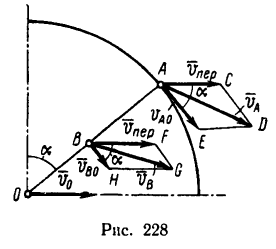
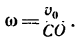
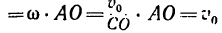
точку С (см. рис. 227), найдем, что Следовательно, с

(так как СО = АО — радиус колеса).

Таким образом, для точки, расположенной на ободе катящегося без скольжения колеса,

^пер — Vao === Последовательно, параллелограмм ACDE есть ромб с углом САЕ = а = 60°, поэтому

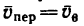
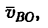
4. Абсолютная скорость vB точки В равна диагонали параллелограмма BFGH, построенного на переносной скорости и па относительной скорости и ее числовое значение можно определить по формуле

Но предварительно необходимо найти скорость 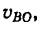которая определяется из соотношения

Задача №4

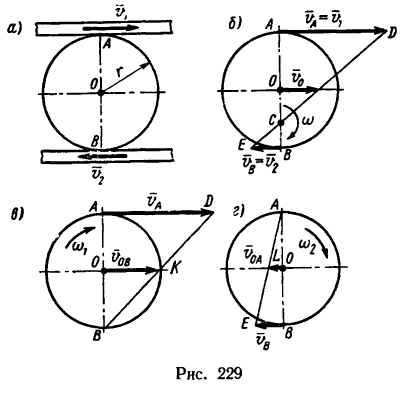
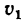
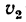
Две параллельные рейки (рис. 229, а) движутся в противоположные стороны с постоянными скоростями = 8 м/сек и = 2 м/сек. Между рейками зажат диск радиусом r = 0,5 м, катящийся по рейкам без скольжения.

Найти угловую скорость диска и скорость его центра.

Решение 1— при помощи мгновенного центра скоростей.

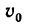
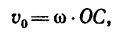
2. Скорость центра диска определяется по формуле

где 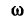— угловая скорость диска.

3. Величины угловой скорости и расстояния ОС находим из равенств:

Так как левые части обоих равенств равны между собой, то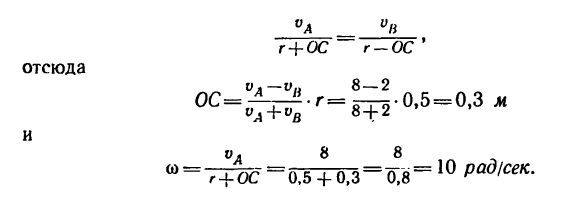

4. Находим скорость

Решение 2—методом последовательной остановки реек.

1. Плоское движение диска образуется вследствие независим мого друг от друга перемещения реек. Поэтому скорость центра диска можно получить как результат геометрического сложения скоростей, получаемых точкой О от перемещения каждой рейки.

2. Мысленно остановим нижнюю рейку (рис. 229,в). Тогда благодаря передвижению верхней рейки диск будет катиться по нижней без скольжения и в точке В образуется мгновенный центр скоростей.

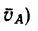
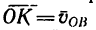
Соединим точку В с точкой D (концом вектора и получим треугольник BAD, в котором вектор изображает скорость центра диска при неподвижной нижней рейке.

Так как ОК — средняя линия треугольника BAD,

Угловая скорость диска в этом движении

3. Теперь мысленно остановим верхнюю рейку (рис. 229 г). Диск будет катиться без скольжения по верхней рейке, имея мгновенный центр скоростей в точке А.

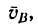
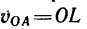
Соединив точку А с концом Е вектора получим треугольник АВЕ, определяющий скорость центра диска при неподвижной верхней рейке.

Угловая скорость диска в этом движении

4. При одновременном движении обеих реек скорость центра диска

так как обе скорости 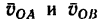направлены вдоль одной прямой, но в противоположные стороны.

5. Угловая скорость диска определяется как сумма угловых скоростей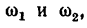найденных выше:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник