что значит направляющие косинусы
Направляющие косинусы вектора.
Определение направляющих косинусов
Направляющие косинусы однозначно задают направление вектора.
Соответственно координатам единичного вектора равны его направляющим косинусам.
Формулы вычисления направляющих косинусов вектора
Формула вычисления направляющих косинусов вектора для плоских задач
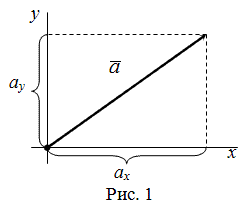
В случае плоской задачи (рис. 1) направляющие косинусы вектора a = < ax ; ay > можно найти воспользовавшись следующей формулой
Формула вычисления направляющих косинусов вектора для пространственных задач
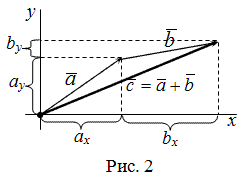
В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = < ax ; ay ; az > можно найти воспользовавшись следующей формулой
Примеры задач с направляющими косинусами вектора
Примеры плоских задач с направляющими косинусами вектора
Найдем модуль вектора a :
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5.
Найдем направляющие косинусы вектора a :
| cos α = | ax | = | 3 | = 0.6 |
| | a | | 5 |
| cos β = | ay | = | 4 | = 0.8 |
| | a | | 5 |
Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.
Примеры пространственных задач с направляющими косинусами вектора
Найдем модуль вектора a :
| a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Направляющие косинусы вектора.
Определение направляющих косинусов
Направляющие косинусы однозначно задают направление вектора.
Соответственно, координаты единичного вектора равны его направляющим косинусам.
Формулы вычисления направляющих косинусов вектора
Формула вычисления направляющих косинусов вектора для плоских задач
В случае плоской задачи (рис. 1) направляющие косинусы вектора a = < ax ; ay > можно найти воспользовавшись следующей формулой
Формула вычисления направляющих косинусов вектора для пространственных задач
В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = < ax ; ay ; az > можно найти воспользовавшись следующей формулой
Примеры задач с направляющими косинусами вектора
Примеры плоских задач с направляющими косинусами вектора
Найдем модуль вектора a :
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5.
Найдем направляющие косинусы вектора a :
| cos α = | ax | = | 3 | = 0.6 |
| | a | | 5 |
| cos β = | ay | = | 4 | = 0.8 |
| | a | | 5 |
Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.
Примеры пространственных задач с направляющими косинусами вектора
Найдем модуль вектора a :
| a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Координаты вектора. Направляющие косинусы
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
Координаты вектора
Сумма двух векторов, заданных координатами
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.
Координаты вектора. Направляющие косинусы не по зубам? Тебе ответит эксперт через 10 минут!
Умножение вектора на число
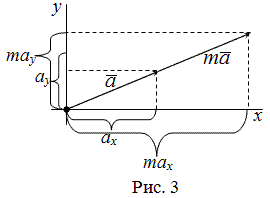
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.
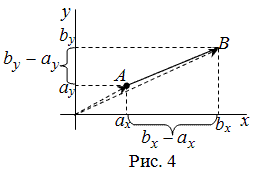
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.
Направляющие косинусы
Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.
Основное свойство направляющих косинусов
Сумма квадратов направляющих косинусов равна единице.
1.8 Направляющие косинусы вектора
§8. Направляющие косинусы вектора.
Рассмотрим еще одну важную характеристику вектора.
Определение 1. Направляющими косинусами вектора а в данном базисе называются косинусы
углов между вектором а и базисными ортами: 
Теорема 1. Направляющие косинусы единичного вектора равны его координатам.
Теорема 2. Сумма квадратов направляющих косинусов равна единице:
<Пусть а = (а1,а2,а3). Обозначим 

Пример. Найти направляющие косинусы вектора а = (4, −2, 4).
Координаты вектора. Направляющие косинусы
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
Пусть даны прямоугольная декартова система координат (ПДСК) \(\ x O y \) и произвольный вектор \(\ \overline \), начало которого совпадает с началом координат системы (рис. 1).
Чтобы найти сумму двух векторов, заданных их координатами, нужно сложить их соответствующие координаты.
Умножить вектор на число
Чтобы умножить вектор на число, необходимо умножить каждую координату этого вектора на данное число.
Далее рассмотрим случай, когда начало вектора не совпадает с началом системы координат. Предположим, что две точки \(\ A\left(a_
Чтобы найти координаты вектора, заданные координатами начала и конца, необходимо вычесть соответствующие координаты начала из координат конца.
Направляющие косинусы вектора называются косинусами углов, образованных вектором с положительными направлениями осей координат.
Здесь \(\ \alpha, \beta \) и \(\ \gamma \) углы, составляющие вектор с положительными направлениями осей \(\ O x, O y \) и \(\ O z \) соответственно.
Основное свойство направления косинусов
Сумма квадратов направляющих косинусов равна единице.
\(\ \cos ^ <2>\alpha+\cos ^ <2>\beta+\cos ^ <2>\gamma=1 \)
Основное свойство направляющих косинусов, сумма их квадратов равна единице