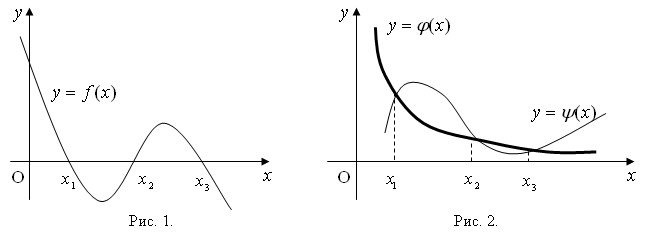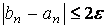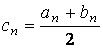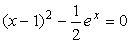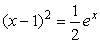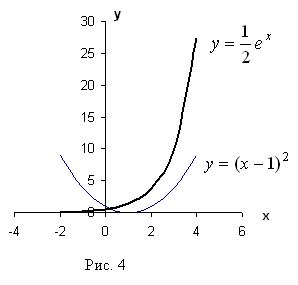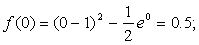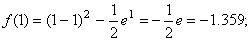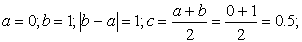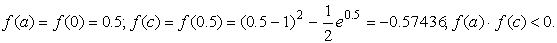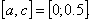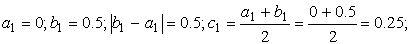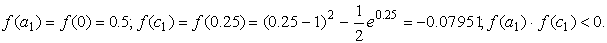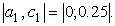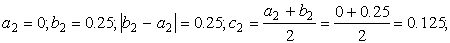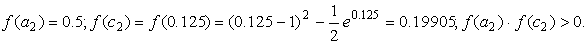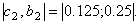что значит найти корень уравнения с точностью

Что значит найти корень уравнения с точностью

1. Приближенное решение нелинейных уравнений

Пусть дано уравнение с одним неизвестным

Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.

Приближенное решение уравнения состоит из двух этапов:

1. Отделение корней, то есть нахождение интервалов из области определения функции f ( x ), в каждом из которых содержится только один корень уравнения (1).

2. Уточнение корней до заданной точности.

Отделение корней можно проводить графически и аналитически.

с точностью ε = 0,0001. Отделим корень графически. Для этого преобразуем уравнение к виду

и построим графики функций (рис. 4):

Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку [0; 1].

Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка [0; 1] имеем:

Уточнение корня выполним методом половинного деления.

Корень принадлежит отрезку

Корень принадлежит отрезку

Корень принадлежит отрезку

Источник

Вычислительная математика копия 1

Уравнение называется алгебраическим, если его можно представить в виде:

Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение f(x)=0 не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.

Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n =1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n >4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.

1.1 Отделение корня

Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.

Корень можно отделить аналитически и графически.

Графический метод отделения корня

1.2 Уточнение корня методом деления отрезка пополам

Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам.

1.3 Метод хорд

Источник

Численное решение нелинейных уравнений с одной переменной

Информатика, 10-11 классы

, ДВГГУ

ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ С ОДНОЙ ПЕРЕМЕННОЙ

При решении задач прикладного характера в разнообразных разделах физики, механики, техники и других областях возникает необходимость решения нелинейных уравнений с одной переменной. При этом многие уравнения не имеют аналитических решений. Это относится к большинству трансцендентных уравнений. Также доказано, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраические уравнение выше четвертой степени.

Уравнение будем называть линейным[1], алгебраическим или трансцендентным в зависимости от того, имеет ли оно одно решение, n решений или неопределенное число решений.

Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). Например, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.[2]

Методы решения нелинейных уравнений делятся на две группы:

Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Далее будут рассмотрены несколько численных методов и приведены алгоритмы нахождения корней уравнений.

В общем случае нелинейное уравнение можно записать в виде:

(1)

(2)

где функции f(x) и g(x) также определены и непрерывны на интервале .

Всякое число обращающее уравнения (1) или (2) в верные числовые равенства называется корнем этого уравнения.

Корни уравнения могут быть действительными и комплексными. В дальнейшем будет идти речь только о вычислении действительных корней.

Решить уравнение численно значит:

1) установить имеет ли оно действительные корни;

2) отделить эти корни (то есть на числовой оси найти достаточно тесные промежутки, называемые интервалами изоляции корня, содержащие только один корень данного уравнения);

3) уточнить отделенные корни, т. е. найти значения корней с заданной степенью точности .

Последнее означает следующее.

Любое число, содержащееся между и , можно принять за приближенное значение корня x* с точностью до .

Графические методы решения уравнений[3]

Пусть дано уравнение F (х) = 0. Построим график функции F (х). Абсциссы точек пересечения графика с осью Ох и являются корнями уравнения. Иногда для графического решения уравнения удобнее записать его в виде и построить графики функций: и Абсциссы точек пересечения этих графиков и являются корнями уравнения F (х) = 0 (рис. 12).

Однако этот метод позволяет получить лишь грубо приближенные значения корней уравнения. Для получения значений корней с большей точностью применяются численные методы. Однако, графи­ческий метод очень удобен, так как он позволяет найти корни с точностью, достаточной для решения многих практических задач, а также достаточно нагляден, прост и доступен.

Численные методы решения уравнений

Наиболее распространенными на практике численными методами решения уравнения (1) являются: метод половинного деления, метод хорд, метод касательных, метод простой итерации и т. д.[4]

Процесс численного решения уравнений разбивается на три этапа:

1. Отделение корней уравнения. Этот процесс можно сделать как графически, так и аналитически. Важно найти такие отрезки, которые бы содержали по одному корню уравнения (1).

2. Выбор метода решения и преобразование уравнения к виду, удобному для применения данного метода.

3. Уточнение корней с заданной точностью при помощи выбранного численного метода.

Говорят, что корень x* уравнения отделен на отрезке , если он содержится в данном отрезке, и если на этом отрезке других корней нет.

Провести полное отделение всех корней уравнения – значит разбить всю область допустимых значений на интервалы (или на отрезки), в каждом из которых содержится ровно по одному корню (или не содержится ни одного корня).

Отделение корней обычно начинают проводить графически. Для этого строят графики функций, получают интервалы, в которых на­ходятся корни уравнения. Это предположение затем проверяют ана­литически, пользуясь следующим свойством непрерывной функции F(x): если функция непрерывна на интервале и на его концах имеет разные знаки (), то между точками a и b имеется хотя бы один корень уравнения . При этом корней может оказаться и несколько, как показано на рис. 13.

Для того чтобы на интервале существовал только один корень, должно выполняться следующее свойство: если функция непрерывна и монотонна на отрезке и принимает на концах отрезка значения разных знаков, то внутри отрезка содержится корень уравнения и этот корень единственный (рис. 14, а, b).

Пример 1: Отделить графически положительные корни уравнения

Решение: Найдем приближенные значения корней уравнения графически. Для этого удобно представить уравнение в следующем виде: e0,3x = 2 sin(2x).

Решением данного уравнения будет являться абсцисса x точки пересечения графиков следующих функций: y1(x) = 2 sin(2x);

На рисунке видно, что графики функций y1(x) и y2(x) пересекаются в двух точках A и B, абсциссы которых положительны и лежат соответственно в промежутках и. Следовательно, уравнение имеет два положительных корня x1 и x2, которые лежат в промежутках и.

Примечание: Графики функций можно строить с помощью компьютера, например, в электронных таблицах Excel или в MathCad.

Пример 2: Отделить аналитически корни уравнения

x3 – 3x2 + 11x + 1 = 0 (4)

Решение: Для аналитического отделения корней найдем производную функции

Производная этой функции

Из таблицы видно, что f(-1)f(0)

Источник

Что значит найти корень уравнения с точностью

Pers.narod.ru. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений

1. Приближенное решение нелинейных алгебраических уравнений

Дано нелинейное алгебраическое уравнение

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

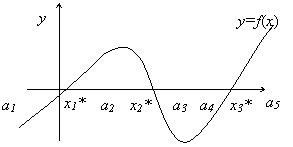
В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что 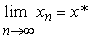. По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 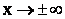и нахождение участков возрастания и убывания функции.

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

X₁=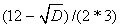= 0.268;

X₂=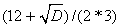= 3.732;

Найдем интервалы изоляции для каждого из корней.

Рассмотрим для второго корня отрезок [1, 3]:

Источник

Приближенное вычисление корней в уравнениях

Приближенное вычисление корней в уравнениях

1.1 Способ хорд (или способ линейной интерполяции).

Приближённое решение уравнений.

Если квадратные уравнения решали уже древние греки, то способы решения алгебраических уравнений третьей и четвёртой степени были открыты лишь в XVI веке. Эти классические способы дают точные значения корней и выражают их через коэффициенты уравнения при помощи радикалов различных степеней. Однако эти способы приводят к громоздким вычислениям и поэтому имеют малую практическую ценность.

В отношении алгебраических уравнений пятой и высших степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как:

На простейших из таких способов мы и остановимся, причём речь будет идти о вычислении действительных корней.

Пусть нужно решить уравнение:

Если обратиться к рисунку, то каждый корень уравнения (1) представляет собой абсциссу точки пересечения графика функции y=f(х)

C осью Ох (рисунок №1)

С помощью графика функции или каким-нибудь иным способом обычно удаётся установить приблизительные значения корней. Это позволяет для каждого корня получить грубые приближения по недостатку и по избытку. Такого рода грубых приближений во многих случаях оказывается достаточно, чтобы, отправляясь от них, получить все значения корня с требуемой точностью. Об этом и пойдёт речь.

Итак, пусть корень Е уравнения (1) «зажат» между двумя его приближениями а и b по недостатку и по избытку а

Способ хорд (или способ линейной интерполяции).

Проведём хорду АВ (рисунок№3) и за первое приближённое значение корня примем абсциссу x1 точки С пересечения хорды с осью Ох.

Уравнение хорды имеет вид:

Рассмотрение всех четырёх случаев, изображённых на рисунке №2, показывает, что точка x1 лежит между a и b с той стороны от Е, где f(х) имеет знак, противоположный знаку f«(х).

x1 = x2-(b- x1)*f(x1)/f(b)-f(x1)

( в формуле (2) заменяем x1 на x2, а на x1 ); значение x2 оказывается между x1 и Е. Рассматриваем отрезок [x2, b] и находим новое приближённое x3, заключённое между x2 и Е и. т. д. В результате получим последовательность а 0

Найдём первое приближённое значение корня по формуле (2):

так как f(1,588)=-0,817 0

Следовательно, искомый корень с точностью до 0,01 равен 1,64.

1.2 Способ касательных (или способ Ньютона).

и поэтому в точке Д:

Из рисунка видно, что x1` лежит между Е и b. С отрезком [a, x1`] поступаем так же, как с отрезком [a, b] ( рисунок №5), и в результате для нового приближённого значения корня получим:

Значение х2` оказывается между Е и x1`. Рассматриваем отрезок [a, х2`] и находим новое приближение х3` и т. д. В результате получим последовательность:

все более точных приближённых значений корня, причём:

Эта формула справедлива для всех четырёх случаев, изображённых на рисунке 32. Для оценки погрешностей полученных приближений можно опять воспользоваться формулой (5), как и в первом случае, легко устанавливается сходимость последовальности x1`, х2`, х3`,…,xn`,… к значению Е

Пример №2. Методом касательных найдём положительный корень уравнения

с точностью до 0,01.

В этом уравнении f(х)=х^4-2x-4, f`(х)=4х^3-2,а f«(х)=12x^2.Так как f(х) и f«(х) при х0 = 1,7 имеют один и тот же знак, а именно:

f(1,7)=0,952>0 и f«(1,7)>0, то применяем формулу:

x1`= х0- f(х0)/ f`( х0), где f`(1,7)=4*1,7^3-2=17,652. Тогда

Применяем второй раз способ касательных:

х2= x1- f(x1)/ f` (x1), где f(x1)= f(1,646)=0,048, f` (1,646) =15,838;

f(1,643)=0,004, f` (1,643)=15,740;

Следовательно, искомый корень с точностью до 0,01 равен 1,64.

1.3 Комбинированный способ

(комбинированное применение способов хорд и касательных).

Этот способ состоит в одновременном использовании способов хорд и касательных. Остановим своё внимание опять на случае, отвечающем первому рисунку №2. Значения x1 и x1`, вычисляем по прежним формулам, т. е. принимаем:

x1`=b-f(b)/f`(b), причём: x1 0 изображён на рисунке №7. Из этого рисунка видно, что уравнение имеет положительный единственный корень, лежащий на отрезке 1 0,f«(x)>0 т. е. знак производных сохраняется. Применяем комбинированный способ:

При этом x1`- x1=0,012, т. е. точность недостаточна. Совершаем второй шаг:

При этом х2`- х2=0,00018, т. е. точность достаточна. Таким образом:

Ошибка в тексте? Выдели её мышкой и нажми

Источник