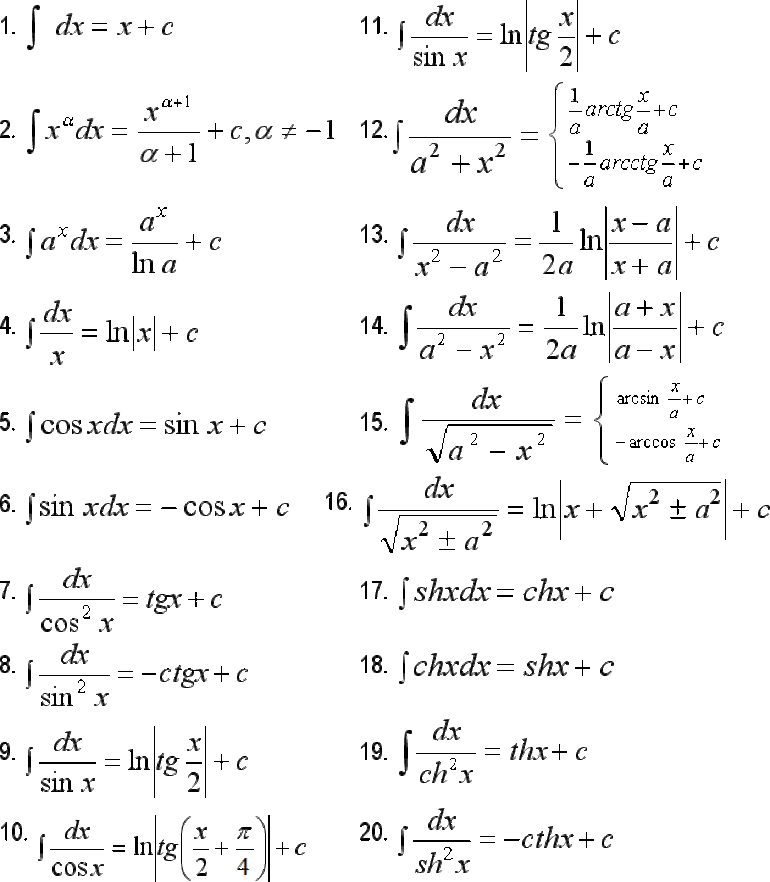что значит найти первообразную для функции

Первообразная функция и неопределенный интеграл

Первообразная

Определение первообразной функции

Можно прочесть двумя способами:

Правила вычисления первообразных

Запомни!

Любая функция F(x) = х 2 + С, где С — произвольная постоянная, и только такая функция, является первообразной для функции f(x) = 2х.

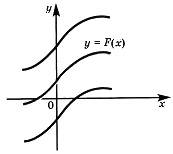
Связь между графиками функции и ее первообразной:

Неопределенный интеграл

Определение:

Свойства неопределённого интеграла

Таблица первообразных и неопределенных интегралов

Функция

Первообразная

F(x) + C

Неопределенные интегралы

\int f(x) dx = F(x) + C

Формула Ньютона–Лейбница

Пусть f (х) данная функция, F её произвольная первообразная.

То есть, интеграл функции f (x) на интервале [a;b] равен разности первообразных в точках b и a.

Площадь криволинейной трапеции

Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.

Площадь криволинейной трапеции находят по формуле Ньютона-Лейбница:

Источник

Первообразная функции

Что такое первообразная функции

Первообразная функции представляет собой такую функцию, производная которой соответствует исходной функции.

К примеру, требуется преобразовать производную, которая имеет следующий вид:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Известна справедливая формула:

Таким образом, можно посчитать заданную производную:

Можно выполнить следующие подробные преобразования для \(x^<2>\)

Исходя из формулировки производной, выражение можно представить и в таком виде:

Таким образом, данная запись является определением первообразной. Для корректной записи следует выполнить следующую операцию:

По аналогии можно записать следующее выражение:

При обобщении этого правила, получится формула:

Выполнив необходимые действия, можно сформулировать определение первообразной.

Основное свойство, сколько первообразных существует для функции

В том случае, когда F(х) представляет собой первообразную функцию f(х), функция F(х) + С, в которой С является произвольной постоянной, также будет первообразной функцией f(х). Таким образом, в математике все первообразные функции f(х) будут записаны в виде F(х) +С. Данное утверждение является основным свойством множества первообразных.

Графически все подобные первообразные данной функции f(х) получают из геометрического графика какой-то одной первообразной с помощью параллельных переносов по порядку вдоль оси Оу.

Первообразная функции и неопределенный интеграл

Неопределенным интегралом от функции f(x) называют выражение F(х)+С, то есть совокупность всех первообразных данной функции f(х).

Обозначение неопределенного интеграла:

Где f(x) представляет собой подынтегральную функцию; f(x) dx —подынтегральное выражение; x представляет собой переменную интегрирования; F(x) является одной из первообразных функции f(x); С является элементарной произвольной постоянной.

Существует несколько характерных для интеграла свойств:

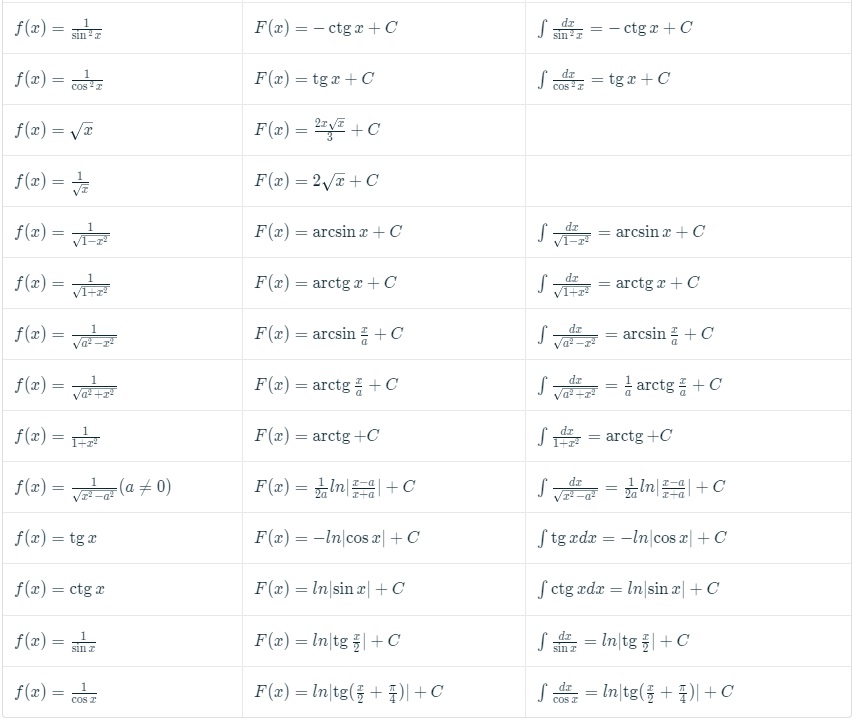
Таблица первообразных с неопределенными интегралами будет иметь следующий вид:

Допустим, что дана функция f(х), F является ее произвольной первообразной. В процессе расчетов можно записать следующее выражение для решения:

Где F(x) представляет собой первообразную для f(x).

Таким образом, интеграл функции f(х) на физическом промежутке (а;b) представляет собой разность первообразных в точках b и а.

Как записать всю совокупность первообразных функций

Элементарная запись выглядит следующим образом:

Где f (x) dx является подынтегральным выражением; f (x) представляет собой подынтегральную функцию; х — это переменная интегрирования; F (x) представляет собой первообразную для функции f (x); С — является некоторой постоянной величиной.

d является знаком дифференциала и обладает двойным назначением:

Таблица первообразных и правила их нахождения

В качестве разъяснения можно использовать пример первообразной:

Данная первообразная для функции:

В качестве подтверждения следует представить производную:

К примеру, необходимо решить пару задач:

Нахождение F(х) выполняют двумя способами:

Можно выполнить проверку:

С помощью простых вычислений можно проверить все строчки таблицы. Таким образом, будет выполняться соотношение:

С помощью специальных правил можно отыскать первообразные. Согласно первому правилу, первообразная суммы равна сумме первообразных. Допустим:

F является первообразной для f.

G является первообразной для g.

Необходимо представить доказательство выражения:

F + G является первообразной для f + g.

Второе правило о постоянном множителе. По условиям задачи:

Где F представляет собой первообразную для f; k является константой.

Требуется подтвердить, что:

kF является первообразной для kf.

Доказать данное выражение можно с помощью определения первообразной и по правилу дифференцирования. Таким образом:

Смысл правила заключается в том, что при известной первообразной для f можно получить первообразную для kf с помощью умножения F на k.

Третье правило можно записать таким образом:

если y = F(x) является первообразной для функции y = f(x),

Источник

Первообразная функции. Формула Ньютона-Лейбница

Функция F(x), для которой f(x) является производной, называется первообразной функции y = f(x). Функции вида у = F(x) + C образуют множество первообразных функции у = f(x).

Сейчас объясним, что это значит.

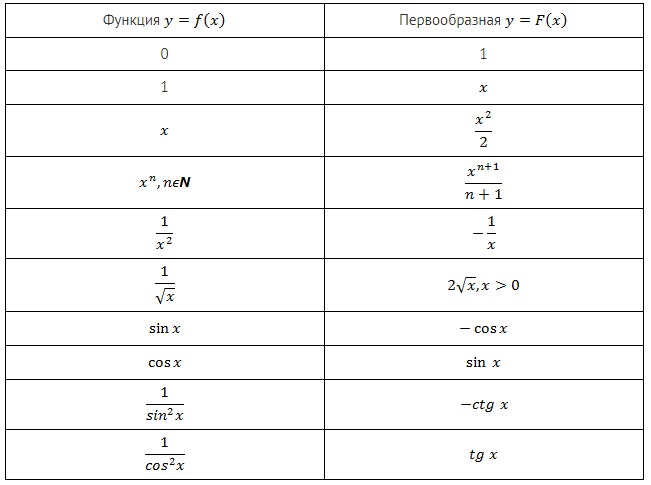
Посмотрим на таблицу первообразных. Каждая функция в левом столбце таблицы является производной для функции в правом столбце.

Таблица первообразных

Первообразная суммы функций равна сумме их первообразных.

Первообразная разности функций — разности первообразных.

Множество всех первообразных функции называется неопределенным интегралом данной функции. Записывается это так:

Нахождение первообразной называется также интегрированием функции. А нахождение производной — дифференцированием функции. Интегрирование (то есть нахождение первообразной) и дифференцирование (взятие производной) — взаимно-обратные действия.

Но интегралы — отдельная тема. В задачах ЕГЭ по математике неопределенные интегралы не встречаются, а теме «Первообразная» посвящено всего несколько задач в первой части ЕГЭ. Для их решения надо знать только таблицу первообразных и еще одну важную формулу.

Формула для вычисления площади под графиком функции (Формула Ньютона-Лейбница)

Тогда площадь этой фигуры вычисляется по формуле:

Такую фигуру называют еще криволинейной трапецией. А сама формула носит название «Формула Ньютона-Лейбница».

Найдем первообразную функции с помощью таблицы первообразных. Получим:

Найдем первообразную функции с помощью таблицы первообразных. Получим:

При x = 0 получим: Значит, и

По формуле Ньютона-Лейбница, разность первообразных — это площадь, ограниченная графиком функции, осью X и прямыми y=a и y=b.

Решение. По формуле Ньютона-Лейбница, площадь под графиком функции на отрезке [a,b] равна разности значений первообразной в концах отрезка, то есть

Источник

Основная информация

Первообразная некоторой функции находится при помощи операции интегрирования. Последняя является обратной для вычисления производной. Например, существует какое-то выражение Z(p). Его производной является некоторая функция z(р), то есть [Z(p)]’ = z(p). Нахождение Z(p) осуществляется по таблице первообразных или интегралов. Когда такой нет под рукой, то можно применить и таблицу производных. При этом следует учитывать константу.

Табличные значения специалисты не рекомендуют заучивать, поскольку такие действия приводят к потере драгоценного времени. Они считают, что в процессе нахождения интегралов информация отложится в голове. Для начала рекомендуется рассмотреть неопределенный интеграл, а затем переходить к другим его видам.

Применение интеграла

Интеграл — один из основных элементов высшей математики. Его обозначают «∫». После этого символа следует подынтегральное выражение, которое записывается в следующем виде: (функция)d(переменная). Следует отметить, что совокупность символов «d(переменная)» обозначает, по какой переменной следует осуществлять операцию интегрирования.

При помощи операции поиска первообразной можно находить площади некоторых фигур, величину пути при неравномерном движении и множество других параметров, для которых невозможно применить общие формулы и соотношения.

Алгебраический смысл интеграла заключается в представлении некоторой суммы в виде маленьких слагаемых. Их бывает много видов: неопределенный, определенный, двойной и так далее. Однако конечным результатом является некоторая производная. Следует отметить, что идет строгое разделение по переменным, по которым выполняется интегрирование. В этом случае их нужно классифицировать на два вида: определенный и неопределенный.

Неопределенным интегралом произвольной функции z(p) называется выражение, представленное в виде ее первообразной с учтенной константой Z(p) + C, то есть ∫(z(p)) dp = Z(p) + С. У него отсутствуют ограничения в виде некоторых числовых значений границ. Первообразная находится в общем виде. Во втором случае также следует найти исходную функцию, но по формуле Ньютона-Лейбница подставляются числовые значения. Далее находится конкретная числовая величина.

Чтобы найти первообразную, необходимо руководствоваться некоторыми правилами. Математики рекомендуют их знать, поскольку это поможет в дальнейшем обучении.

Методика нахождения

Существуют определенные правила нахождения первообразных. Для нахождения интеграла простейшей функции необходимо воспользоваться таблицей первообразных (рис. 1). Далее нужно найти соответствующее выражение и записать результат. Однако задания не всегда могут быть простыми, поскольку некоторые выражения следует упростить, а другие — решаются только при помощи формул интегрирования по частям.

Рисунок 1. Таблица первообразных.

Методика нахождения первообразной для простой табличной функции состоит из двух этапов. Для этой цели следует воспользоваться обыкновенным алгоритмом, который рекомендуют математики всего мира:

Если первый метод не подходит, то следует воспользоваться формулой первообразной, которая позволяет выполнять операцию интегрирования по частям. Прибегать к такому варианту следует в том случае, когда функция является сложной и ее нет в таблицах производных и интегралов.

Суть соотношения заключается в упрощении сложного выражения и сведении его к табличному значению. Следует отметить, что методика может применяться много раз и без каких-либо ограничений. Специалисты выделили отдельные подынтегральные функции, к которым нужно применять эту методику:

Если по какой-то причине интеграл невозможно взять, то это объясняется только наличием ошибок при интегрировании. Специалисты рекомендуют пересмотреть ход решения или начать его заново. Иногда необходимо осуществить замену подынтегрального выражения, но этот способ не будет рассматриваться, поскольку он является очень сложным.

Геометрический смысл

У интеграла есть определенный геометрический смысл, который заключается в нахождении площади криволинейной трапеции. К последним принадлежат плоские фигуры, ограниченные некоторым заданным графиком, а также прямыми или другими графиками. Основные требования — непрерывность и конечное значение S (площади) должно быть больше нуля. Как правило, в подынтегральную часть идет сама функция, а границами являются значения переменных.

В качестве ограничителей могут выступать также и оси декартовой системы координат. Чтобы вычислить площадь этой фигуры, необходимо выполнить такие операции:

Проверив результат при расчетах и на калькуляторе интегралов, можно сделать вывод, что задача решена правильно. Кроме того, следует проверять подынтегральное выражение. Например, если дана функция с корнем четной степени (квадрат, четвертая и так далее), то необходимо указывать, что функция должна быть больше или равна 0.

Источник

Первообразная и неопределенный интеграл, их свойства

Определение первообразной

Определение неопределенного интеграла

Имея заданный дифференциал функции, мы можем найти неизвестную функцию.

∫ f ( x ) d x ‘ = F ( x ) + C ‘ = f ( x )

∫ d ( F ( x ) ) = ∫ F ‘ ( x ) d x = ∫ f ( x ) d x = F ( x ) + C

∫ f ( x ) ± g ( x ) ) d x = ∫ f ( x ) d x ± ∫ g ( x ) d x

Промежуточные равенства первого и второго свойств неопределенного интеграла мы привели в качестве пояснения.

Для того, чтобы доказать третье и четвертое свойства, необходимо найти производные от правых частей равенств:

k · ∫ f ( x ) d x ‘ = k · ∫ d ( x ) d x ‘ = k · f ( x ) ∫ f ( x ) d x ± ∫ g ( x ) d x ‘ = ∫ f ( x ) d x ‘ ± ∫ g ( x ) d x ‘ = f ( x ) ± g ( x )

Производные правых частей равенств равны подынтегральным функциям, что является доказательством первого свойства. Его же мы используем в последних переходах.

Как видите, задача интегрирования представляет собой обратный процесс по отношению к задаче дифференцирования. Обе эти задачи тесно связаны между собой.

Первое свойство может быть использовано для проведения проверки интегрирования. Для проверки нам достаточно вычислить производную полученного результата. Если полученная функция будет равна подынтегральной функции, то интегрирование проведено верно.

Благодаря второму свойству по известному дифференциалу функции мы можем найти ее первообразную и использовать ее для вычисления неопределенного интеграла.

Решение

Используя таблицу производных основных элементарных функций получаем

d ( ln x ) = ( ln x ) ‘ d x = d x x = f ( x ) d x ∫ f ( x ) d x = ∫ d x x = ∫ d ( ln ( x ) )

Ответ: f ( x ) = 1 x = ln ( x ) + 1

Необходимо найти неопределенный интеграл ∫ 2 sin x 2 cos x 2 d x и проверить результат вычисления дифференцированием.

Решение

Используем таблицу производных для тригонометрических функций, получим:

Проверим полученный результат дифференцированием.

В результате проверки мы получили подынтегральную функцию. Это значит, что интегрирование было проведено нами верно. Для осуществления последнего перехода мы использовали формулу синуса двойного угла.

Если таблицу производных основных элементарных функций переписать в виде дифференциалов, то из нее по второму свойству неопределенного интеграла можно составить таблицу первообразных.

Подробнее эту тему мы рассмотрим в следующем разделе «Таблица первообразных (таблица неопределенных интегралов)».

Источник