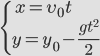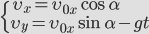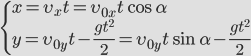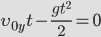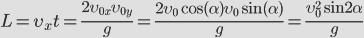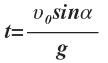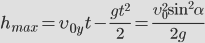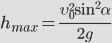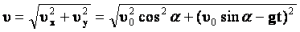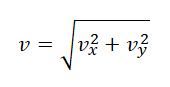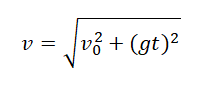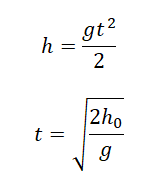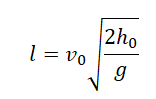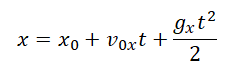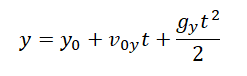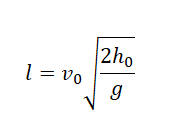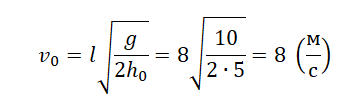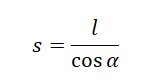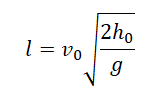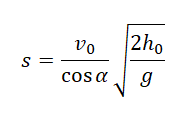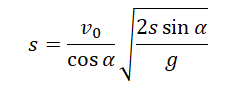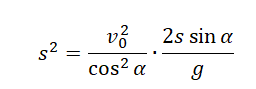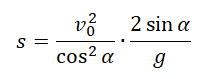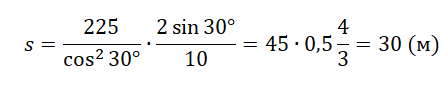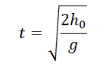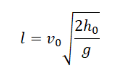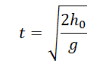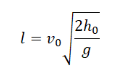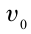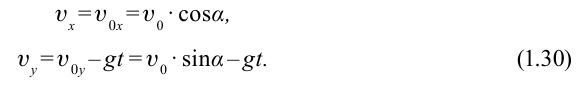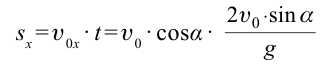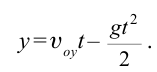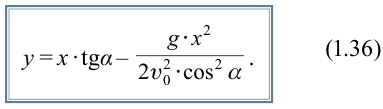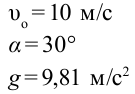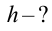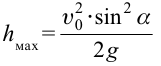что значит под углом к горизонту

Тело, брошенное под углом к горизонту: типы траекторий, формулы

Каждый из нас бросал камни в небо и наблюдал за траекторией их падения. Это самый распространенный пример движения твердого тела в поле гравитационных сил нашей планеты. В данной статье рассмотрим формулы, которые могут пригодиться для решения задач на свободное движение тела, брошенного к горизонту под углом.

Понятие о движении к горизонту под углом

Вам будет интересно: Явление фотоэффекта. Красная граница фотоэффекта. Пример решения задачи

Тип движения под углом изучает баллистика.

Свойства рассматриваемого типа движения

Когда рассматривают траекторию движения тела в поле гравитационных сил Земли, то оказываются справедливыми следующие утверждения:

Отметим, что указанные свойства справедливы, если сила трения в процессе полета тела пренебрежимо мала. В баллистике при изучении полетов снарядов учитывают много разных факторов, в том числе и трение.

Типы параболического движения

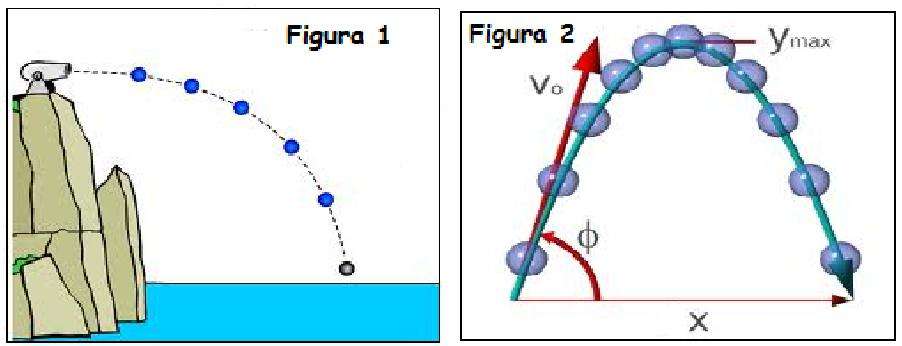
В зависимости от того, с какой высоты начинается движение, на какой высоте заканчивается, и как направлена начальная скорость, выделяют следующие типы параболического движения:

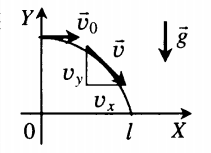
График движения тела, соответствующий полной параболе, приведен выше.

Необходимые для расчета формулы

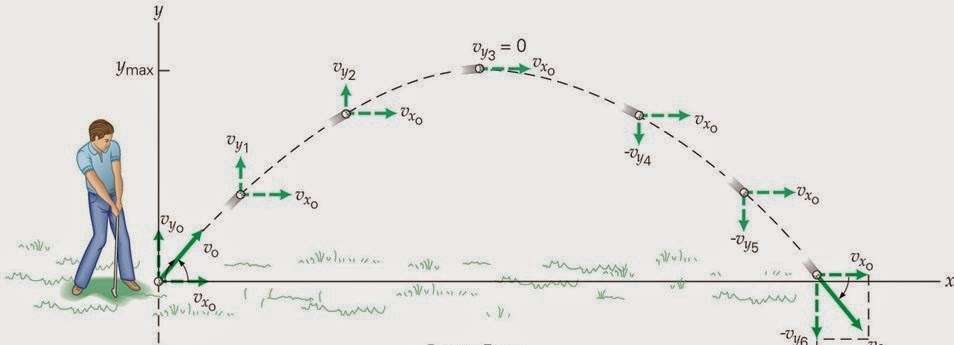
Приведем формулы для описания движения тела, брошенного под углом к горизонту. Пренебрегая силой трения, и учитывая только силу тяжести, можно записать два уравнения для скорости перемещения объекта:

Так как сила тяжести направлена вертикально вниз, то горизонтальную компоненту скорости vx она не изменяет, поэтому в первом равенстве отсутствует зависимость от времени. Компонента vy в свою очередь испытывает влияние силы тяжести, которая сообщает g ускорение телу, направленное к земле (отсюда знак минус в формуле).

Теперь запишем формулы для изменения координат тела, брошенного под углом к горизонту:

Теперь выразим время t из первого выражения и подставим его во второе, получим:

Это выражение в геометрии соответствует параболе, ветви которой направлены вниз.

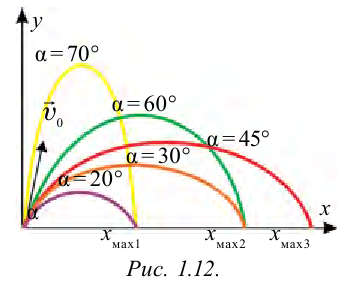
Приведенных уравнений достаточно, чтобы определить любые характеристики этого типа движения. Так, их решение приводит к тому, что максимальная дальность полета достигается, если θ = 45o, максимальная же высота, на которую поднимется брошенное тело, достигается при θ = 90o.

Источник

Движение тела, брошенного горизонтально или под углом к горизонту.

Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.

Движение тела, брошенного горизонтально.

Выразим проекции скорости и координаты через модули векторов.

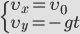
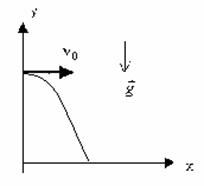
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:

— между координатами квадратичная зависимость, траектория – парабола!

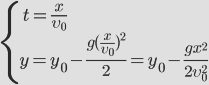
Движение тела, брошенного под углом к горизонту.

Порядок решения задачи аналогичен предыдущей.

Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):

.

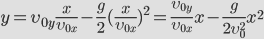
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Следовательно, для решения этой задачи необходимо решить уравнение

Зная время полета, найдем максимальное расстояние, которое пролетит тело:

Дальность полета:

Из этой формулы следует, что:

— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ;

— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.

Тогда:

Максимальная высота:

Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна

Угол, под которым направлен вектор скорости в любой момент времени:

Источник

Движение тела, брошенного горизонтально

теория по физике 🧲 кинематика

Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.

Кинематические характеристики движения

Графически движение горизонтально брошенного тела описывается следующим образом:

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:

Минимальная скорость в течение всего времени движения равна начальной скорости: v_min = v₀.

Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: v_max = v.

Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:

h₀ — высота, с которой тело бросили в горизонтальном направлении.

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид :

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?

Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:

Выразим начальную скорость и вычислим ее:

Горизонтальный бросок тела с горы

Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.

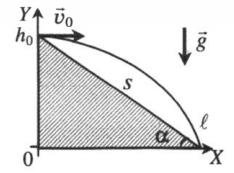
График горизонтального броска тела с горы

α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения

Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:

Начальная высота — высота, с которой было брошено тело. Обозначается h₀. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:

Пример №2. На горе с углом наклона 30 о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?

Выразим это расстояние через дальность полета:

Дальность полета выражается по формуле:

Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:

Выразим с учетом формулы начальной высоты:

Поделим обе части выражения на общий множитель s:

Подставим известные значения:

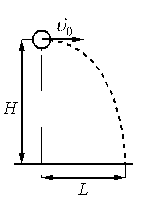
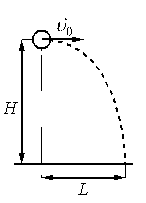
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ ₀, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).

В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2 υ ₀.

Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Время полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.

Дальность полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.

Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.

Значит, верный ответ — 313.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Шарик, брошенный горизонтально с высоты H с начальной скоростью υ ₀, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).

Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Время полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.

Дальность полета тела, брошенного горизонтально, определяется формулой:

Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).

Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.

Значит, верный ответ — 323.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Движение тела, брошенного под углом к горизонту:

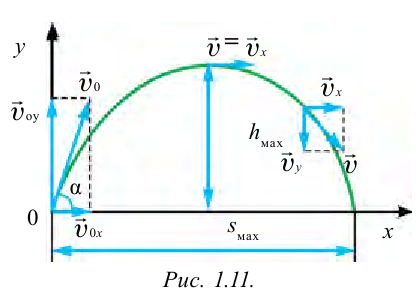
Если рассмотреть движение тела, брошенного под углом относительно горизонта, можно увидеть, что тело отдаляется горизонтально от точки броска и одновременно поднимается в вертикальном направлении. Значит, тело, брошенное под углом к горизонту, участвует в двух (горизонтальном и вертикальном) видах движения. В горизонтальном направлении тело движется равномерно. В вертикальном направлении до точки максимальной высоты тело будет двигаться равнозамедленно, затем вниз будет двигаться равноускоренно (рис. 1.11).

Траектория движения тела, брошенного под углом к горизонту, имеет вид параболы. Учитывая, что в процессе полета тело одновременно двигается в горизонтальном и вертикальном направлениях, разделим начальную скорость

Для упрощения расчетов пренебрежем сопротивлением воздуха. В произвольный момент времени 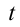перемещение тела в горизонтальном направлении находим из следующего уравнения:

В произвольный момент времени t скорость тела в горизонтальном и вертикальном направлениях можно найти из следующих уравнений:

На протяжении движения тела, брошенного под углом к горизонту, горизонтальная составляющая скорости не меняется, вертикальная составляющая при подъеме является равнозамедленной и на максимальной высоте подъема равняется нулю. Значит, тело, брошенное под углом к горизонту, имеет минимальную скорость в высшей точке траектории:

Затем из этой точки тело движется как тело, брошенное горизонтально со скоростью .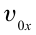
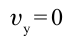
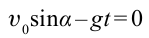
Из соотношения или на максимальной высоте траектории находим время подъема:

Максимальная высота подъема тела определяется следующим соотношением:

Время движения тела вниз (падение) равно времени подъема, т.е. 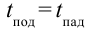. Отсюда, общее время полета:

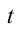
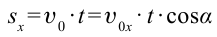
Тело, брошенное под углом к горизонту, в горизонтальном направлении движется равномерно. По этой причине длина полета тела зависит только от горизонтальной составляющей скорости. Для определения дальности полета подставим выражение времени полета в выражение и получим:

Из этого выражения видно, что длина полета тела, брошенного под углом к горизонту, зависит от угла броска. На рис. 1.12 приведена зависимость длины полета и высоты подъема от угла броска. Из рисунка видно, что с увеличением угла броска увеличивается высота подъема.

подставляем выражение для времени полета 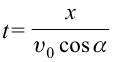из уравнения (1.29) и получаем уравнение траектории в следующем виде:

Образец решения задачи:

Мяч брошен со скоростью 10 м/с под углом 30° к горизонту. На какую высоту поднимется мяч?
Дано:

Решение: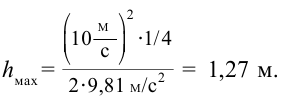

Ответ: 1,27 м.

Основные понятия, правила и законы

Научное наблюдение	Метод научного исследования системный, активный, направленный на цель.
Гипотеза	Предположение о каком-либо процессе, явлении.
Опыт (эксперимент)	Проводится для проверки гипотезы в специальных условиях.
Модель	Упрощенная версия физического процесса, сохраняющая его главные черты.
Научная идеализация	Предсказание получаемого результата в идеальных условиях по ранее полученным результатам.
Научная теория	Набор законов, объясняющий широкую область явлений.
Принцип соответствия	В определенных рамках соответствие новой и старой теорий.
Криволинейное равномерное движение	Движение, траектория которого представляет собой кривую линию, величина скорости не меняется, а направление изменяется по касательной к траектории.
Принцип независимости или суперпозиция движения	Движения, в которых участвует тело, независимы друг от друга, и скорости (ускорение) их движения не зависят друг от друга.
Вертикальное движение вверх	Движение, противоположное силе притяжения Земли. Уравнение движения: .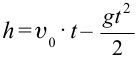
Вертикальное движение вниз	Движение в направлении силы притяжения Земли. Уравнение движения: .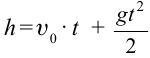
Переменное вращательное движение	Вращательное движение, при котором с течением времени меняется угловая скорость.
Угловое ускорение	Величина, определяемая отношением изменения угловой скорости ко времени этого изменения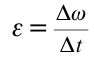
Формула определения угловой скорости в произвольный момент времени при вращательном равнопеременном движении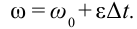
Тангенциальное ускорение	Ускорение, получаемое в связи с изменением величины скорости .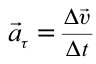
Полное ускорение при криволинейном движении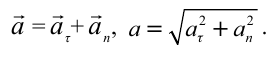
Передача движения фрикционным способом	Движение, передаваемое с помощью действующих поверхностей двух колес с разными радиусами.
Ременная передача движения	Движение передается от одного колеса к другому через туго натянутый ремень.
Передача движения через зубчатые колеса	Передача вращательного движения путем объединения двух зубчатых колес с разными диаметрами.
Дальность полета и скорость при падении горизонтально брошенного тела.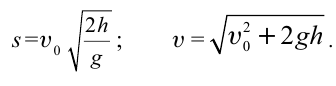
Минимальная скорость тела, брошенного под углом к горизонту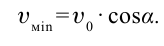
Высота подъема тела, брошенного под углом к горизонту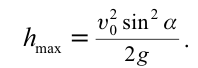
Время полета тела, брошенного под углом к горизонту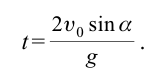
Дальность полета тела, брошенного под углом к горизонту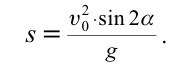
Уравнение траектории движения тела, брошенного горизонтально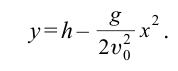
Уравнение траектории движения тела, брошенного под углом к горизонту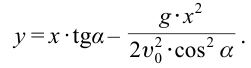

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник