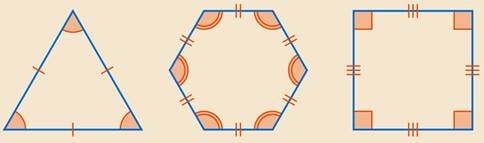
что значит правильный многоугольник

Правильный многоугольник

Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.

В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.

Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

Многогранник размерности 3 и выше называется изоэдральным или гране транзитивным, если все его грани одинаковы. Точнее сказать, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая отображает A в B. По этой причине выпуклые изоэдральные многогранники имеют формы правильных игральных костей.

Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.

Источник

Правильный многоугольник

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

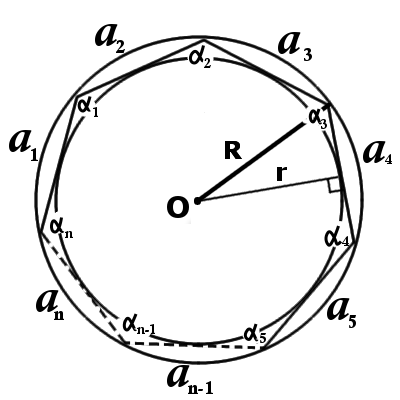
α 1 = α 2 = α 3 = … = α n-1 = α n

где a₁ … a_n — длины сторон правильного многоугольника,
α ₁ … α _n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2 · r · tg 180° n (через градусы),

a = 2 · r · tg π n (через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2 · R · sin 180° n (через градусы),

a = 2 · R · sin π n (через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a : 2 · tg 180° n (через градусы),

r = a : 2 · tg π n (через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a : 2 · sin 180° n (через градусы),

R = a : 2 · sin π n (через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

Формула площади n-угольника через радиус вписанной окружности

Формула площади n-угольника через радиус описанной окружности

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

Формула площади правильного треугольника через длину стороны

Формула площади правильного треугольника через радиус вписанной окружности

Формула площади правильного треугольника через радиус описанной окружности

Углы между сторонами правильного треугольника

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

Углы между сторонами правильного четырехугольника

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через радиус вписанной окружности

Формула площади правильного шестиугольника через радиус описанной окружности

Углы между сторонами правильного шестиугольника

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

Источник

Свойства правильного многоугольника

В данной публикации мы рассмотрим основные свойства правильного многоугольника касательно его внутренних углов (в т.ч. их суммы), количества диагоналей, центра описанной и вписанной окружностей. Также рассмотрены формулы для нахождения основных величин (площадь и периметр фигуры, радиусы окружностей).

Примечание: определение правильного многоугольника, его признаки, основные элементы и виды мы рассмотрели в отдельной публикации.

Свойства правильного многоугольника

Свойство 1

Внутренние углы в правильном многоугольнике ( α ) равны между собой и могут быть рассчитаны по формуле:

где n – число сторон фигуры.

Свойство 2

Свойство 3

Количество диагоналей (D_n) правильного n-угольника зависит от количества его сторон (n) и определяется следующим образом:

Свойство 4

В любой правильный многоугольник можно вписать круг и описать окружность около него, причем их центры будут совпадать, в том числе, с центром самого многоугольника.

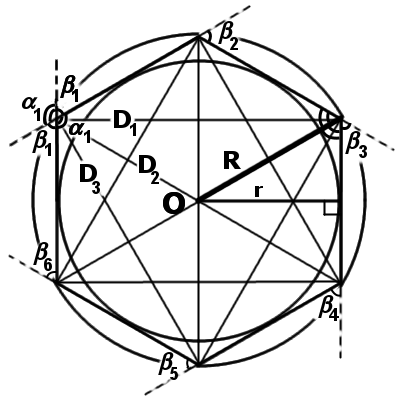
В качестве примера на рисунке ниже изображен правильный шестиугольник (гексагон) с центром в точке O.

Площадь (S) образованного окружностями кольца вычисляется через длину стороны (a) фигуры по формуле:

Между радиусами вписанной (r) и описанной (R) окружностей существует зависимость:

Свойство 5

Зная длину стороны (a) правильного многоугольника можно рассчитать следующие, относящиеся к нему величины:

1. Площадь (S):

2. Периметр (P):

3. Радиус описанной окружности (R):

4. Радиус вписанной окружности (r):

Свойство 6

Площадь (S) правильного многоугольника можно выразить через радиус описанной/вписанной окружности:

Источник

Определение правильного многоугольника

Правильный многоугольник — что значит

Многоугольник представляет собой часть площади, ограниченную замкнутой ломаной линией, которая не пересекает сама себя.

Многоугольники различают по количеству сторон и углов.

Правильный многоугольник обладает одинаковыми сторонами и углами.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Существует несколько разновидностей правильных многоугольников. К наиболее известным относят равносторонний треугольник, который обладает тремя одинаковыми сторонами и углами, равными 60 градусов. В связи с этим данную геометрическую фигуру называют правильным треугольником.

Квадрат обладает четырьмя одинаковыми сторонами и углами по 90 градусов. Такую геометрическую фигуру называют правильным четырехугольником.

В геометрии можно встретить фигуры с одинаковыми сторонами и разными углами, к примеру, ромб. Существуют фигуры, углы которых равны, но стороны различны по длине. К данному типу относится прямоугольник. Важно отметить, что прямоугольник и ромб не являются правильными многоугольниками.

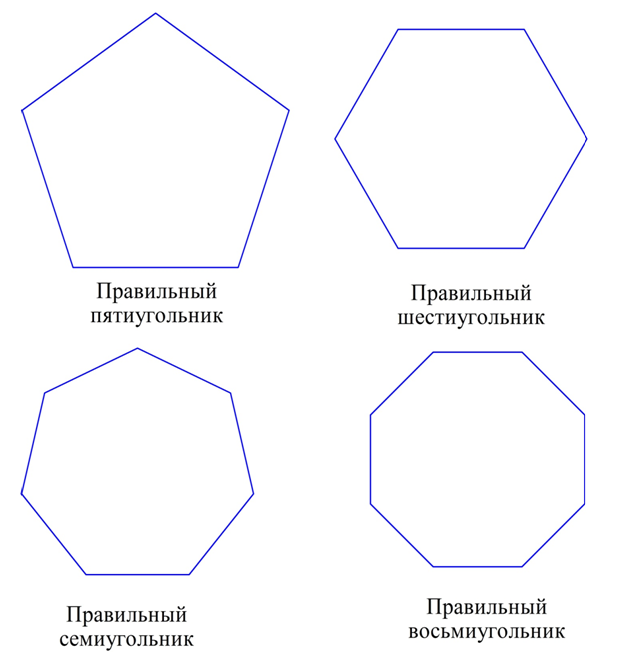
При каком-либо заданном числе n, начиная с n=3, можно построить правильный n-угольник. Примеры таких многоугольников изображены на рисунке:

Признаки и свойства правильного многоугольника

Многоугольник можно считать правильным в том случае, когда все его стороны и углы одинаковы. Таким образом, должно выполняться правило:

\(\alpha _ <1>= \alpha _ <2>= \alpha _ <3>= … = \alpha _ = \alpha _\)

Существуют основные свойства, характерные для правильных многоугольников.

Основные свойства, определение правильного n-угольника

Правильный n-угольник представляет собой особый вид многоугольника с равными между собой сторонами и углами.

Существует формула, с помощью которой можно определить его длину при известном радиусе вписанной в него окружности:

При этом радиус вписанной окружности n-угольника определяют через длину стороны:

Сторону правильного n-угольника можно определить на основании радиуса описанной вокруг него окружности:

Таким образом, радиус описанной окружности n-угольника составляет:

Площадь правильного n-угольника можно определить, зная длину стороны, по формуле:

При известном радиусе вписанной окружности, площадь n-угольника равна:

Если известен радиус описанной окружности, то площадь n-угольника определяется по формуле:

Периметр правильного n-угольника составляет:

Определить угол между сторонами правильного n-угольника можно с помощью формулы:

Известно, что треугольник можно задать с помощью длин трех его сторон. Однако в случае правильного треугольника необходимо знать только одну длину стороны, так как все правильные треугольники подобны. Таким образом, при отсутствии данных о масштабе или метрики, правильные треугольники эквивалентны друг другу.

Такими же свойствами обладает квадрат, то есть правильный четырехугольник.

В качестве примеров таких геометрических фигур можно рассмотреть правильные пяти, шести и сколь угодно большие n-угольники. Предельным случаем при бесконечно увеличивающемся n является окружность. Для всех таких многоугольников характерны следующие свойства:

В геометрии можно встретить разные виды правильных n-угольников. Все они обладают не только одним параметром, с помощью которого задаются, но и характеризуются осями и центром симметрии. Правильный треугольник возможно три раза повернуть вокруг центра. При этом разница между данными положениями отсутствует.

Квадрат можно повернуть таким же способом четыре раза. Предельным случаем является окружность, которую можно повернуть бесконечное число раз, но результат при этом не изменится, то есть данная геометрическая фигура обладает бесконечным количеством осей симметрии.

В природе невозможно найти идеальную окружность или любой другой правильный n-угольник. В реальности предметы рассматривают лишь в качестве их приближений. Однако многие практические задачи характеризуются достаточно точным приближением, что позволяет применять правильные многоугольники в их решении, как полезный инструмент. Свойства таких геометрических фигур изучают и фиксируют.

В дальнейшем при рассмотрении окружности в качестве предельного случая правильных n-угольников эти свойства переносят на нее для получения полезных утверждений не для ломаной, а для гладкой кривой.

Известно, что равносторонний треугольник представляет собой правильный треугольник. Необходимо выяснить, является ли любой равносторонний многоугольник также правильным многоугольником.

В качестве примера можно рассмотреть ромб, имеющий равные стороны. Таким образом, ромб является равносторонним четырехугольником, но не относится к правильным n-угольникам. К данной категории справедливо отнести только квадрат, так как он обладает не только равными сторонами, но и углами, что отличает его от ромба.

Напомним, что правильными многоугольниками являются те, которые имеют равные стороны и равные углы.

В случае треугольника достаточным условием является равенство сторон. Так как из этого следует равенство его углов. При рассмотрении других n-угольников это утверждение не верно.

Формула угла правильного многоугольника

В данном случае n обозначает число сторон многоугольника.

Используя данную закономерность можно определить углы других правильных многоугольников.

Угол правильного пятиугольника равен:

Угол правильного шестиугольника составляет:

Угол правильного восьмиугольника равен:

В случае правильного многоугольника с 50 углами, каждый угол составит:

Далее в качестве примера использования формулы угла правильного n-угольника можно рассмотреть задачу на определение числа сторон у правильного многоугольника, каждый угол которого составляет \(179^<0>.\)

Таким образом, рассматриваемый правильный многоугольник обладает 360 сторонами.

Исходя из того, что число сторон является не целым, а дробным, можно сделать вывод о невозможности существования такого многоугольника.

Источник

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

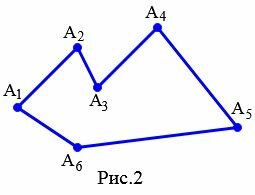На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

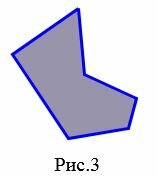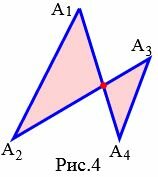На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

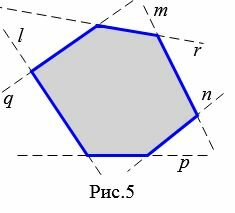На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

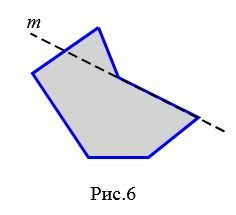На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

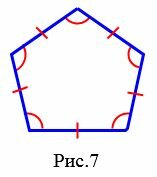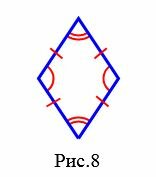На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

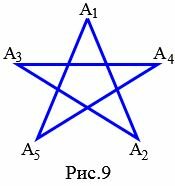На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

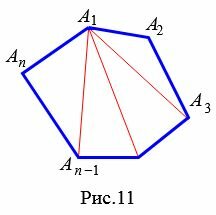Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Источник