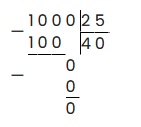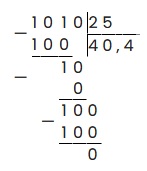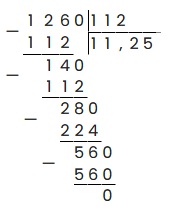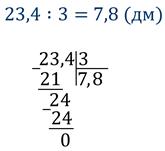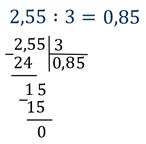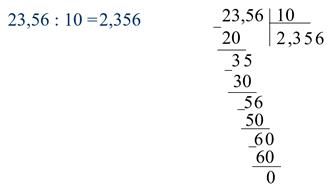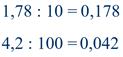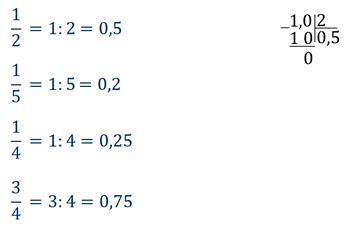что значит разделить десятичную дробь на натуральное число
Деление десятичных чисел
Перед тем как перейти к вопросу, о том, как делить десятичные дроби, вспомним теоретические основы. Итак:
Десятичная дробь — это представление обыкновенной дроби в десятичной форме, где знаменатель равен 10, 100, 1000 и т.д. Другими словами, десятичная дробь — это результат деления числителя на знаменатель. К примеру, ½ = 0,5.
Как делить десятичные дроби?
Деление десятичных дробей сводится к делению обыкновенных дробей. Рассмотрим подробнее основные правила деления десятичных дробей.
Деление десятичной дроби на натуральное число
Напомним, что натуральные числа — это числа, которые мы используем в повседневной жизни, для подсчета (1, 2, 3, 4 и т.д). Алгоритм деления натурального числа на десятичную дробь в столбик, выглядит так:
Чтобы разделить десятичную дробь на натуральное числа используем стандартный алгоритм деления в столбик.
Пример 1: Разделить 100 на 2,5.
Согласно вышеприведенному алгоритму, избавимся от запятой. Таким образом добавим к 100 один 0 и получим 1000 : 25. Решение будет выглядеть так:
Пример 2: Разделить 101 на 2,5.
Аналогично предыдущему примеру, избавимся от запятой. Таким образом получим 1010 : 25, где решение:
Ответ: 101 : 2.5 = 40.4
Пример 3: Разделить 7.5 на 3.
В этом примере, деление осуществляется по стандартному алгоритму деления столбиком. Таким образом:
Как делить десятичную дробь на целое число?
Производим вычисления, по алгоритму деления натурального числа на десятичную дробь, не обращая внимания на знаки (чтобы не запутаться знаки можно не писать):
Из правила следует, что плюс разделить на минус будет минус, таким образом:
Деление двух десятичных дробей
Деление двух десятичных чисел сводится к предыдущему алгоритму, т.е. необходимо избавиться от запятых. В случае, если в делителе, цифр после запятой больше чем в делимом, необходимо в делимое добавить соответствующее количество нулей.
Пример 5: Разделить 12,6 на 1,12.
Т.к. в делителе (1,12) две цифры после запятой, то для избавления от запятых, необходимо в делимом (12,6), добавить ноль, таким образом:
Ответ: 12.6 : 1.12 = 11.25
Деление десятичных дробей на 10, 100, 1000
Правило деления десятичной дроби на 10, 100, 1000 и т.д. состоит в том, что для получения ответа, необходимо в этой дроби перенести запятую влево на столько цифр, сколько нулей в делителе после единицы.
Деление десятичных дробей на 0,001, 0,01, 0,1
Правило деления десятичной дроби на 0,001, 0,01, 0,1 и т.д. состоит в том, что для получения ответа, необходимо в этой дроби перенести запятую вправо на столько цифр, сколько нулей в делителе перед единицей.
Деление десятичных дробей на натуральные числа
Урок 36. Математика 5 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Деление десятичных дробей на натуральные числа»
На этом уроке мы узнаем, как правильно делить десятичные дроби. А также узнаем, какими правилами пользуются при делении десятичных дробей.
Муравей пробегает за 3 минуты 23,4 дм. Какое расстояние пробежит муравей за 1 минуту?
Разделить десятичную дробь на натуральное число означает найти такую дробь, которая при умножении на данное натуральное число даёт делимое.
Этот же ответ можно получить и не занимаясь переводом одних величин в другие. Для этого необходимо выполнить деление не обращая внимание на запятую. И не забыть поставить запятую в частном, когда закончится деление целой части, т.е.
Запомним правило, которым мы будем пользоваться при делении десятичных дробей на натуральные числа:
1) Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую.
2) Ставим в частном запятую, когда заканчивается деление целой части делимого.
Найдите значения выражений:


Есть и ещё случаи, которые могут затруднить вас в решении. Давайте и их рассмотрим, чтобы потом было легче решать.
Разделим число 23,56 на 10.
Запомним ещё одно правило: чтобы разделить десятичную дробь на 10, 100, 1000 и т.д. надо перенести запятую в этой дроби на столько цифр влево, сколько нулей записано после единицы в делителе.
При этом иногда следует записать перед целой частью нуль или несколько нулей.
С помощью деления можно перевести обыкновенную дробь в десятичную.
Чтобы разделить десятичную дробь на натуральное число надо:
1) разделить десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую.
2) поставить в частном запятую, когда заканчивается деление целой части делимого.
Если целая часть делимого меньше делителя, то в частном пишут нуль целых.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д. надо перенести запятую в этой дроби на столько цифр влево, сколько нулей записано после единицы в делителе.
Деление десятичных дробей
б) Если целая часть делимого больше делителя, то разделите целую часть нацело или с остатком, поставьте запятую в ответе (после полученного числа).
2. Продолжите деление далее как деление натуральных чисел (записывая результат после запятой).
Не забываем записывать ответ в пример:
Попробуйте разделить сами: 12,42:180
Должно получиться 0,069
При делении натуральных чисел можно пользоваться этим же алгоритмом, помня, что любое натуральное число можно представить в виде десятичной дроби, поставив в конце него запятую и написав некоторое количество нулей в виде десятичных знаков. Например, 5=5,0 или 5=5,000 или 5=5,000000
Давайте попробуем разделить!
Выразите 265 мм в сантиметрах, дециметрах, метрах.
(Решение: 265 мм = 26,5 см, т. к. 265:10=26,5 ( , на 1 знак влево)
265 мм = 2,65 дм, т. к. 265:100=2,65 ( , на 2 знака влево)
265 мм = 0,265 м, т. к. 265:1000=0,265 ( , на 3 знака влево))
Например, 3,14:10=0,314 и 3,14*0,1=0,314
В основе деления десятичной дроби на десятичную дробь лежит деление десятичной дроби на натуральное число.
Давайте потренируемся: 0,237 : 0,03=23,7 : 3 (в делителе 0,03 две цифры после запятой, значит переносим запятую на две позиции вправо и в делителе (получается 3), и в делимом (получается 23,7). Наша задача, чтобы в делителе не было десятичной дроби, чтобы было натуральное число!)
4,5 : 0,125 = 4500 : 125 (в делителе 0,125 три цифры после запятой, значит надо перенести запятую и в делителе, и в делимом на три позиции вправо. В делителе получается натуральное число 125. А в делимом не хватает цифр при переносе запятой вправо, поэтому дописали справа недостающее количество нулей. Получилось 4500)
3,876 : 0,02 = 387,6 : 2 (В делителе 0,02 две цифры после запятой, значит переносим запятую и в делителе, и в делимом на две позиции вправо. Получилось в делителе натуральное число 2, а в делимом 387,6)
71,55 : 0,0045 = 715500 : 45
Попробуйте сами: 2,728 : 0,44
3. Разделите полученное число на натуральное по алгоритму деления десятичной дроби на натуральное число (см. пункт I)
Математика. 6 класс
Конспект урока
Деление положительных десятичных дробей. Часть 1
Перечень рассматриваемых вопросов:
Десятичная дробь – это дробь, у которой знаменатель является степенью числа 10.
Десятичные дроби записывают без знаменателей, выделяя целую часть (целая часть правильной дроби считается равной 0) и отделяя её запятой от числителя дробной части.
Чтобы разделить десятичную дробь на натуральное число, нужно разделить дробь на это число, не обращая внимания на запятую, а в частном поставить запятую в тот момент, когда закончится деление целой части делимого.
Чтобы разделить десятичную дробь на десятичную, надо:
– перенести в делимом и в делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
– выполнить деление на натуральное число.
Чтобы записать обыкновенную дробь в виде десятичной, нужно числитель этой дроби разделить на знаменатель.
Теоретический материал для самостоятельного изучения
Частное двух десятичных дробей всегда можно записать в виде обыкновенной дроби. В то же время не любая обыкновенная дробь может быть записана как десятичная. На этом уроке мы рассмотрим только такие случаи, когда частное есть десятичная дробь или натуральное число.
Рассмотрим несколько примеров, в которых десятичную дробь мы делим на натуральное число.
1,2 : 3 = 0,4, так как 0,4 · 3 = 1,2
2,4 : 8 = 0,3, так как 0,3 · 8 = 2,4
Но это случаи, когда деление можно выполнить устно. А что делать в случаях, когда устные вычисления невозможны?
Деление десятичных дробей будем производить так же, как и деление натуральных чисел – уголком.
Рассмотрим деление 42,12 на 18
Запишем деление уголком и будем делить, не обращая внимания на запятую. При этом запятую в частном поставим в тот момент, когда спишем первую цифру после запятой в делимом.
Проверим получившийся ответ.
Деление выполнено верно.
Если целая часть делимого меньше делителя, то целая часть частного равна нулю.
4 целых разделить нацело на 13 нельзя, поэтому пишем 0. Производим вычитание и списываем из делимого первую цифру после запятой, и сразу ставим запятую в частном. Продолжаем выполнять деление. Получаем
Рассмотрим ещё один пример.
Мы остановили процесс деления, так как закончились цифры в делимом. При этом ноль в остатке мы ещё не получили. Вспомните, что справа после последней цифры в десятичной дроби можно приписать бесконечное количество нулей, от этого десятичная дробь не изменится. Получаем
Теперь мы можем находить частное от деления двух натуральных чисел даже в случае, если делимое не делится нацело на делитель.
Выполняем деление, помня о том, что 21 = 21,0000. Списывая первую цифру из дробной части, ставим запятую.
Итак, мы разобрались с делением десятичной дроби на целое число. Теперь рассмотрим деление на десятичную дробь.
Если делимое и делитель одновременно увеличить в 10,100,1000 и так далее раз, то частное не изменится. Это следует из основного свойства обыкновенной дроби.
Значит, для того, чтобы разделить 12,88 на 4,6, нужно делимое и делитель одновременно умножить на 10, получим: 12,88:4,6 = 128,8 : 46. То есть в результате получим деление на натуральное число.
Таким образом, можно представлять обыкновенную дробь в виде десятичной. Помним, что дробная черта аналогична знаку деления.
Задача. Поезд проехал 138,6 км за 2,8 часов. Какое расстояние он проедет за 6,2 часа с той же скоростью?
Найдём скорость движения поезда. Для этого пройденное расстояние разделим на время пути.
138,6 км : 2,8 ч = 49,5 (км/ч) – скорость поезда.
Найдём расстояние, которое поезд проедет за 6,2 часа. Для этого скорость поезда умножим на время пути.
49,5 км/ч · 6,2 ч = 306,9 (км).
Ответ: 306,9 км – расстояние, которое проедет поезд за 6,2 часа.
Задача. Моторная лодка проплыла 20,08 км по течению реки и 41,23 км против течения. Сколько времени плыла лодка, если её собственная скорость равна 23,4 км/ч, а скорость течения равна 1,7 км/ч?
Сначала найдём скорость лодки по течению, для этого к скорости течения прибавим собственную скорость лодки.
23,4 км/ч + 1,7 км/ч = 25,1 (км/ч) – скорость по течению.
Найдём скорость против течения. Для этого из скорости лодки вычтем скорость течения.
23,4 км/ч – 1,7 км/ч = 21,7 (км/ч) – скорость против течения.
Найдём время, за которое лодка проплыла путь по течению. Для этого расстояние, пройденное по течению, разделим на скорость движения по течению.
20,08 км : 25,1 км/ч = 0,8 (ч) – время, которое плыла лодка по течению.
Найдём время, за которое лодка проплыла путь против течения. Для этого расстояние, пройденное против течения, разделим на скорость движения против течения.
41,23 км : 21,7 км/ч = 1,9 (ч) – время, которое плыла лодка против течения.
Найдём общее время нахождения лодки в пути.
1,9 ч + 0,8 ч = 2,7 (ч) – всего плыла лодка.
Ответ: лодка находилась в пути 2,7 ч.
Разбор заданий тренировочного модуля
Вычислите значение выражения и впишите правильный ответ.
168 : 0,7 – 9,28 : 11,6 – 30 : 96 + 0,1125 = …
Десятичные дроби
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.