что значит целочисленное деление
Что значит целочисленное деление
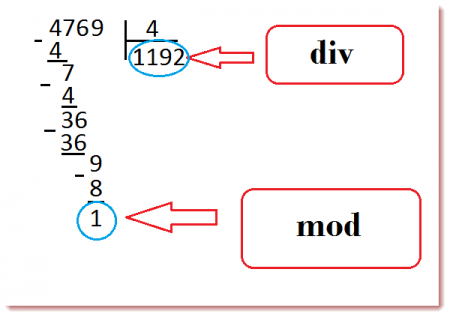
Оператор div и оператор mod
В этой статье речь пойдет о целочисленном делении и делении с остатком.
То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.
Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e
Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так
z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!
А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.
Например (40 / 6) с остатком = 4 с оператором mod будет такой
Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.
Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим
Целочисленное деление
Смотреть что такое «Целочисленное деление» в других словарях:
Деление с остатком — Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число.… … Википедия
целочисленное умножение и деление — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN integer multiplication and division … Справочник технического переводчика
SIGFPE — Описание: Ошибочная арифметическая операция По умолчанию: завершение с дампом памяти коды SA SIGINFO FPE INTDIV Целочисленное деление на нуль FPE INTOVF Целочисленное переполнение FPE FLTDIV Деление на нуль с плавающей запятой FPE FLTOVF… … Википедия
Троичная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Обработка исключений — Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Проставив сноски, внести более точные указания на источники … Википедия
Digital Signature Standard — DSS, Digital Signature Standard Создатель: NIST Создан: август 1991 Опубликован: 19 мая 1994 Размер ключа: 512 1024 бит Размер подписи: два числа по 160 бит DSS (Digital Signature Standard) американский стандарт, описывающий Digital Si … Википедия
Python — У этого термина существуют и другие значения, см. Python (значения). Python Класс языка: му … Википедия
Befunge — Befunge стековый эзотерический язык программирования. Считается двумерным, так как программа на Befunge записывается в таблицу со сшитыми краями (тор), по которой в различных направлениях перемещается интерпретатор, исполняя команды,… … Википедия
MetaPost — Класс языка: императивный Появился в … Википедия
Piet — «Hello World» на языке Piet Piet эзотерический язык программирования разработанный Давидом Морган Маром. Язык Piet использует разноцветные изображения в качестве программ. Программа на Piet выглядит как постживописная абстракция. Piet… … Википедия
Целочисленная арифметика. Делим с округлением результата. Часть 1
Чем проще, на первый взгляд, задача, тем меньше разработчик вдумывается в то, как грамотно её реализовать, и допущенную ошибку, в лучшем случае, обнаруживает поздно, в худшем — не замечает вовсе. Речь пойдет об одной из таких задач, а именно, о дробном делении и о масштабировании в контроллерах, поддерживающих исключительно целочисленную арифметику.
Почему тонкостям вычислений в условиях такой арифметики разработчики прикладных программ не уделяют внимание, вопрос. Рискну только предположить, что, по всей вероятности, сказывается привычка производить вычисления на калькуляторе… Во всяком случае, с завидной регулярностью «имею счастье» лицезреть, как коллеги по цеху наступают на одни и те же грабли. Этот материал нацелен на то, чтобы те самые «грабли» нейтрализовать.
При целочисленной арифметике результат деления одного целого числа на другое состоит из двух чисел — частного и остатка. Если остаток деления отбросить, получим результат, в абсолютной величине округленный до меньшего целого.
Реализуя вычисления с дробями, этот момент частенько упускают из вида, а, упустив, получают потери в точности вычислений. Причем точность вычислений падает с ростом величины делителя. К примеру, что 53/13, что 64/13 дадут в результате 4, хотя, по факту, частное от деления второй дроби существенно ближе к 5.
На самом деле, округление результата до ближайшего целого организовать элементарно. Для этого достаточно удвоить остаток деления, просуммировав его сам с собою, а затем вновь поделить его на то же число, на которое делили первоначально, и частное от этого деления сложить с частным, полученным от первоначальной операции деления.
Принимая во внимание то, что такие вычисления в программе могут потребоваться неоднократно, алгоритм вычислений реализуем в формате, пригодном для упаковки в подпрограмму.
Для корректного выполнения необходимых для этого промежуточных вычислений понадобится массив из пяти регистров, обозначим его условно TEMP[0..4]. Почему пять и не меньше, поясню чуть ниже.
Шаги с 3-го по 7-й могут быть вынесены в подпрограмму.
При желании, запись результата может быть произведена непосредственно суммированием TEMP[0] c TEMP[1] за пределами подпрограммы расчета. Это непринципиально. Единственное, следует иметь в виду, что при множестве однотипных расчетов вынос операции сложения в основное тело программы способен привести к возрастанию задействованного ею объема программной памяти.
Так почему же для промежуточных вычислений потребовалось целых 5 регистров? А операция суммирования остатка деления самого с собой, о чем говорилось ранее, заменена умножением остатка на два? Очень просто — для того, чтобы оперировать с неограниченным набором целых чисел.
То бишь, удвоенный остаток от целочисленного деления дроби в интересах округления результата такого деления всегда должен быть представлен в формате double integer.
Делись, рыбка, быстро и нацело
Деление — одна из самых дорогих операций в современных процессорах. За доказательством далеко ходить не нужно: Agner Fog[1] вещает, что на процессорах Intel / AMD мы легко можем получить Latency в 25-119 clock cycles, а reciprocal throughput — 25-120. В переводе на Русский — МЕДЛЕННО! Тем не менее, возможность избежать инструкции деления в вашем коде — есть. И в этой статье, я расскажу как это работает, в частности в современных компиляторах(они то, умеют так уже лет 20 как), а также, расскажу как полученное знание можно использовать для того чтобы сделать код лучше, быстрее, мощнее.
Собственно, я о чем: если делитель известен на этапе компиляции, есть возможность заменить целочисленное деление умножением и логическим сдвигом вправо (а иногда, можно обойтись и без него вовсе — я конечно про реализацию в Языке Программирования). Звучит весьма обнадеживающе: операция целочисленного умножения и сдвиг вправо на, например, Intel Haswell займут не более 5 clock cycles. Осталось лишь понять, как, например, выполняя целочисленное деление на 10, получить тот же результат целочисленным умножением и логическим сдвигом вправо? Ответ на этот вопрос лежит через понимание… Fixed Point Arithmetic (далее FPA). Чуть-чуть основ.
При использовании FP, экспоненту (показатель степени 2 => положение точки в двоичном представлении числа) в числе не сохраняют (в отличие от арифметики с плавающей запятой, см. IEE754), а полагают ее некой оговоренной, известной программистам величиной. Сохраняют же, только мантиссу (то, что идёт после запятой). Пример:
0.1 — в двоичной записи имеет ‘бесконечное представление’, что в примере выше отмечено круглыми скобками — именно эта часть будет повторяться от раза к разу, следуя друг за другом в двоичной FP записи числа 0.1.
В примере выше, если мы используем для хранения FP чисел 16-битные регистры, мы не сможем уместить FP представление числа 0.1 в такой регистр не потеряв в точности, а это в свою очередь скажется на результате всех дальнейших вычислений в которых значение этого регистра участвует.
Пусть дано 16-битное целое число A и 16-битная Fraction часть числа B. Произведение A на B результатом дает число с 16 битами в целой части и 16-тью битами в дробной части. Чтобы получить только целую часть, очевидно, нужно сдвинуть результат на 16 бит вправо.
Поздравляю, вводная часть в FPA окончена.
Формируем следующую гипотезу: для выполнения целочисленного деления на 10, нам нужно выполнить умножение Числа Делимого на FP представление числа 0.1, взять целую часть и дело в шля… минуточку… А будет ли полученный результат точным, точнее его целая часть? — Ведь, как мы помним, в памяти у нас хранится лишь приближенная версия числа 0.1. Ниже я выписал три различных представления числа 0.1: бесконечно точное представление числа 0.1, обрезанное после 16-ого бита без округления представление числа 0.1 и обрезанное после 16 ого бита с округлением вверх представление числа 0.1.
Оценим погрешности truncating представлений числа 0.1:
Чтобы результат умножения целого числа A, на Аппроксимацию числа 0.1 давал точную целую часть, нам нужно чтобы:
Удобнее использовать первое выражение: при мы всегда получим тождество (но, заметь, не все решения, что в рамках данной задачи — более чем достаточно). Решая, получаем
. То есть, умножая любое 14-битное число A на truncating with rounding up представление числа 0.1, мы всегда получим точную целую часть, которую бы получили умножая бесконечно точно 0.1 на A. Но, по условию у нас умножается 16-битные число, а значит, в нашем случае ответ будет неточным и довериться простому умножению на truncating with rounding up 0.1 мы не можем. Вот если бы мы могли сохранить в FP представлении числа 0.1 не 16 бит, а, скажем 19, 20 — то все было бы ОК. И ведь можем же!
Внимательно смотрим на двоичное представление — truncating with rounding up 0.1: старшие три бита — нулевые, а значит, и никакого вклада в результат умножения не вносят (новых бит).
Следовательно, мы можем сдвинуть наше число влево на три бита, выполнить округление вверх и, выполнив умножение и логический сдвиг вправо сначала на 16, а затем на 3 (то есть, за один раз на 19 вообще говоря) — получим нужную, точную целую часть. Доказательство корректности такого ’19’ битного умножения аналогично предыдущему, с той лишь разницей, что для 16-битных чисел оно работает правильно. Аналогичные рассуждения верны и для чисел большей разрядности, да и не только для деления на 10.
В регистре RCX пусть хранится некое целое 62-битное A, а в регистре RAX пускай хранится 64 битное FA представление truncating with rounding up числа 0.1 (заметь, никаких сдвигов влево нету). Выполнив 64-битное умножение получим, что в регистре RDX сохранятся старшие 64 бита результата, или, точнее говоря — целая часть, которая для 62 битных чисел, будет точной. То есть, сдвиг вправо (SHR, SHRX) не нужен. Наличие же такого сдвига нагружает Pipeline процессора, вне зависимости поддерживает ли он OOOE или нет: как минимум появляется лишняя зависимость в, скорее всего и без того длинной цепочке таких зависимостей (aka Dependency Chain). И вот тут, очень важно упомянуть о том, что современные компиляторы, видя выражение вида some_integer / 10 — автоматически генерируют ассемблерный код для всего диапазона чисел Делимого. То есть, если вам известно что числа у вас всегда 53-ех битные (в моей задаче именно так и было), то лишнюю инструкцию сдвига вы получите все равно. Но, теперь, когда вы понимаете как это работает, можете сами с легкостью заменить деление — умножением, не полагаясь на милость компилятору. К слову сказать, получение старших битов 64 битного произведения в C++ коде реализуется интринсиком (something like mulh), что по Asm коду, должно быть равносильно строчкам инструкции MUL
Возможно, с появлением контрактов (в С++ 20 не ждем) ситуация улучшится, и в каких-то кейсах, мы сможем довериться машине! Хотя, это же С++, тут за все отвечает программист — не иначе.
Рассуждения описанные выше — применимы к любым делителям константам, ну а ниже список полезных ссылок:
Что значит целочисленное деление
Меню
Предметы
Олимпиады
Обратная связь
Разное
Сейчас на сайте
Авторизация
Рассмотрим задачи на целочисленное деление.
Эти задачи важны для составления эффекивных алгоритмов, поэтому нужно научиться решать простейшие с использованием целочисленного деления.
Деление может выполняться только для целых чисел.
Демонстрация их работы:
Задача 1. Определите, сколько целых тонн в массе, выраженной в килограммах. Значение массы в килограммах введите с клавиатуры.
Begin
Вид результата работы программы:
Задача 2. Дано расстояние в сантиметрах. Выразите его в метрах и сантиметрах.
Составьте программу, чтобы она удовлетворяла формату ввода и формату вывода по образцу:
Ввод:
Вывод:
Вид результата работы программы:
Задача 3. В классе а учеников. В столовой им выдали n конфет. По сколько конфет получил каждый? Сколько конфет остались нераспределенными?
Ввод:
Вывод:
Вид результата работы программы:
Рассмотрим задачи на определение цифр числа.
Например, дано трехзначное число 452.
Задача 4. Найдите сумму первой и последней цифры четырехзначного числа. Мы должны получить первую цифру, затем последнюю и найти сумму.