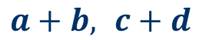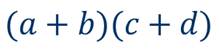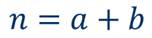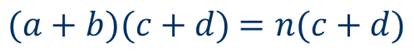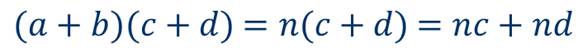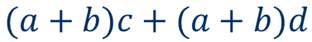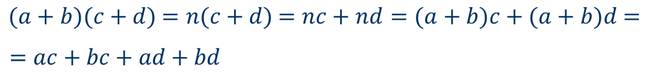что значит умножить многочлен на многочлен

Действия с многочленами

Мы уже разобрали, что из себя представляют многочлены. В рамках данной статьи мы расскажем, как правильно вычитать, умножать, складывать и делить подобные выражения, а также как возводить их в натуральную степень, т.е. определим правила совершения данных действий с многочленами.

Правила сложения и вычитания многочленов

Складывать и вычитать многочлены достаточно просто. Оба эти действия рассматриваются вместе, поскольку осуществляются по одним и тем же принципам:

Поясним алгоритм примером.

Сначала выполним сложение. Записываем сумму:

( 7 · x 2 − 1 ) + ( x · y − x 2 + 2 )

Раскрываем скобки и получаем новый многочлен в следующей форме:

7 · x 2 − 1 + x · y − x 2 + 2

Нам осталось только привести результат к стандартному виду:

7 · x 2 − 1 + x · y − x 2 + 2 = 6 · x 2 + 1 + x · y

Далее проводим вычитание по аналогии со сложением:

( 7 · x 2 − 1 ) − ( x · y − x 2 + 2 ) = 7 · x 2 − 1 − x · y + x 2 − 2 = 8 · x 2 − 3 − x · y

Другие примеры вы можете найти в отдельной статье, посвященной сложению и вычитанию многочленов.

Правила умножения одного многочлена на другой

Перейдем к рассмотрению следующего действия – умножения. Основное правило его выполнения основано на распределительном свойстве умножения. С его помощью мы можем свести умножение многочленов к последовательному перемножению всех их членов друг на друга. Запишем правило:

Чтобы умножить один многочлен на другой, необходимо выполнить умножение каждого члена первого множителя на каждый член второго множителя, после чего провести сложение итоговых произведений.

Результатом умножения двух многочленов друг на друга будет новый многочлен.

Начнем с записи произведения.

a · ( − 3 · a ) + a · b − b · ( − 3 · a ) − b · b = − 3 · a 2 + 4 · a · b − b 2

Вот запись всего решения:

( a − b ) · ( − 3 · a + b ) = = a · ( − 3 · a ) + a · b − b · ( − 3 · a ) − b · b = = − 3 · a 2 + 4 · a · b − b 2

Мы также можем выполнить умножение многочлена на одночлен. Это можно рассматривать как частный случай умножения, приведенного выше. Советуем прочесть отдельную статью об умножении многочленов, где представлены более подробные теоретические положения и приведены более сложные примеры.

Правила возведения многочлена в степень

Условие: выполните возведение многочлена 2 · a · b − b 3 в квадрат.

представим эту степень как произведение двух одинаковых множителей и вычислим нужный результат.

( 2 · a · b − b 3 ) 2 = = ( 2 · a · b − b 3 ) · ( 2 · a · b − b 3 ) = = 2 · a · b · ( 2 · a · b ) + 2 · a · b · ( − b 3 ) − b 3 · ( 2 · a · b ) − b 3 · ( − b 3 ) = = 4 · a 2 · b 2 − 4 · a · b 4 + b 6

Подводя итог этого пункта, отметим, что возведение в степень можно выполнять намного быстрее, если пользоваться формулами сокращенного умножения. Советуем вам изучить эту тему более подробно.

Правила деления многочлена на многочлен

Это так, потому что равенство 3 · x 4 + 2 · x 2 − 1 = ( x 2 + x ) · ( 3 · x 2 − 3 · x + 5 ) − 5 · x − 1 является справедливым. Его справедливость легко проверить, выполнив все нужные действия с правой стороны.

Удобно производить деление, предварительно сделав запись уголком, так же, как мы делаем это для целых чисел. Подробнее это действие разобрано в статье, посвященной делению многочлена на многочлен.

Источник

Умножение многочлена на многочлен – как правильно решать такие задачи?

Многочлены — пространные буквенно-числовые выражения, которые очень часто встречаются в алгебраических примерах и задачах. Такие выражения не только складывают между собой или вычитают друг из друга — но и находят для них произведения.

Перемножить два, три и более многочленов достаточно просто. Математическое действие производится согласно нескольким правилам, и если подойти к задаче внимательно, то ответ удастся получить быстро.

Перемножение многочленов — как выполнить?

Чтобы понять, по какому принципу осуществляется действие, необходимо обратиться к более ранним темам — и вспомнить, что любой многочлен состоит из двух и более одночленов. Из этого естественным образом следует, что для нахождения общего произведения нужно перемножить все части одного многочлена на части другого многочлена — а потом сложить между собой полученные произведения.

Если разбирать ситуацию на примере, то выглядеть она будет следующим образом. Для примера возьмем многочлен a + c и умножим его на многочлен b + d.

Все, что остается сделать дальше — это подставить нужные числа на место переменных, произвести конкретное перемножение, сложить полученные результаты — и записать произведение двух многочленов.

Если по условиям задачи нужно перемножить не два, а более многочленов, то сначала необходимо найти произведение между первыми двумя частями выражения — а потом умножить это произведение на следующую часть все по тем же правилам.

Источник

Умножение многочлена на многочлен: правило, примеры.

Продолжаем изучать действия с многочленами. В этой статье мы разберем умножение многочлена на многочлен. Здесь мы получим правило умножения, после чего рассмотрим его применение при решении примеров на умножение многочленов различного вида.

Навигация по странице.

Правило

Чтобы подойти к правилу умножения многочлена на многочлен, рассмотрим пример. Возьмем два многочлена a+b и c+d и выполним их умножение.

Из проведенных рассуждений можно сделать два важных вывода. Во-первых, результатом умножения многочлена на многочлен является многочлен. Это утверждение справедливо для любых умножаемых многочленов, а не только для тех, которые мы взяли в примере. Во-вторых, произведение многочленов равно сумме произведений каждого члена одного многочлена на каждый член другого. Отсюда следует, что при умножении многочленов, содержащих m и n членов соответственно, указанная сумма произведений членов будет состоять из m·n слагаемых.

Теперь сделанные выводы нам позволяют сформулировать правило умножения многочленов:
чтобы провести умножение многочлена на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и сложить полученные произведения.

Примеры умножения многочлена на многочлен

На практике при решении примеров правило умножения многочлена на многочлен, полученное в предыдущем пункте, разбивается на последовательные шаги:

Разберемся с этим на конкретном примере.

Стоит заметить, что если умножаемые многочлены заданы в виде, отличном от стандартного, то перед умножением их целесообразно привести к стандартному виду. В результате получится тот же результат, что и при умножении многочленов в исходном не стандартном виде, но решение получится намного короче.

Многочлен дан не в стандартном виде. Прежде чем выполнять умножение, приведем многочлен его к стандартному виду:

Теперь можно выполнять умножение многочленов:

.

В заключение скажем, что иногда приходится выполнять умножение трех, четырех и большего количества многочленов. Оно сводится к последовательному умножению двух многочленов. То есть, сначала умножаются первые два многочлена, полученный результат умножается на третий многочлен, этот результат умножается на четвертый многочлен и так далее.

Источник

Что значит умножить многочлен на многочлен

Ключевые слова конспекта: произведение многочленов, умножение одночлена на многочлен, умножение многочлена на многочлен.

1. Умножение одночлена на многочлен

Пусть требуется умножить одночлен 2а 3 на многочлен 3а 4 – 4а 2 + а.
Составим произведение 2а 3 (3а 4 – 4а 2 + а).

При умножении одночлена на многочлен пользуются следующим правилом:

Распределительный закон умножения относительно сложения, на котором основано правило умножения одночлена на многочлен, древнегреческий математик Евклид в III в. до н.э. доказывал на языке «геометрической алгебры»: если одна из сторон прямоугольника является суммой нескольких отрезков, то площадь всего прямоугольника можно найти как сумму площадей его частей. Например, если а = а 1 + а 2 + а 3 – одна сторона прямоугольника, b – его вторая сторона, то площадь прямоугольника равна ab = (ах + а 2 + а 3 )b = ах 6 + а 2 b + а 3 b. Если считать а = а 1 + а 2 + а 3 многочленом, а b – одночленом, то мы получим правило умножения многочлена на одночлен.

В рассмотренном примере мы представили произведение одночлена и многочлена в виде многочлена. Вообще произведение одночлена и многочлена всегда можно представить в виде многочлена. Причём степень произведения будет равна сумме степеней одночлена и данного многочлена.

Пример 1. Умножим одночлен –3ху на многочлен 2х 2 у + 4ху 2 – 1.
Имеем:
–3ху • (2х 2 у + 4ху 2 – 1) = –3ху • 2х 2 у + (–3ху) • 4ху 2 + (–3ху) • (–1) = –6х 3 у 2 – 12х 2 у 3 + 3ху.

Запись можно вести короче, не выписывая промежуточные результаты:
–3ху • (2х 2 у + 4ху 2 – 1) = –6х 3 у 2 – 12х 2 у 3 + 3ху.

Каждое из произведений преобразуем в многочлен и сложим полученные многочлены:
4а(2а + 5) + 2а(3а – 1) – 1,5а(2а – 4) = 8а 2 + 20а + 6а 2 – 2а – 3а 2 + 6а = 11а 2 + 24а.

2. Умножение многочлена на многочлен

Пусть требуется умножить многочлен а + b на многочлен с + d. Составим произведение этих многочленов:
(а + b)(c + d).

Обозначим двучлен а + b буквой х и воспользуемся правилом умножения одночлена на многочлен:
(а + b)(с + d) = х(с + d) = хс + xd.

В выражение хс + xd подставим вместо х многочлен а + b и снова воспользуемся правилом умножения одночлена на многочлен:
хс + xd = (а + b)c + (а + b)d = ас + bc + ad + bd.

Итак,
(а + b)(c + d) = ас + bc + ad + bd.

Этот же результат для положительных а, b, с, d можно увидеть на рисунке, интерпретируя, вслед за Евклидом, произведение двучленов как площадь прямоугольника.

Произведение (а + b)(с + d) мы представили в виде многочлена ас + bc + ad + bd. Этот многочлен является суммой всех одночленов, которые получаются при умножении каждого члена многочлена а + b на каждый член многочлена с + d.

Мы пришли к следующему правилу:

При умножении многочлена а + b на многочлен с + d мы снова получили многочлен. Вообще произведение двух любых многочленов можно представить в виде многочлена. При этом если многочлен, содержащий m членов, умножается на многочлен, содержащий n членов, то в произведении получается многочлен, состоящий из mn членов (до приведения подобных членов). Этим удобно пользоваться для самоконтроля.

Пример 1. Умножим 3а 2 – 4аb + b 2 на многочлен 2а – b.

Умножение многочленов можно выполнять в столбик.

Из приведённого примера можно сделать полезный вывод: степень произведения многочленов равна сумме степеней многочленов–множителей. Действительно, первый множитель – многочлен степени 2, второй – двучлен степени 1, а их произведение – многочлен степени 2 + 1 = 3.

Рассмотрим пример умножения двух многочленов с одной переменной.

Пример 2. Представим в виде многочлена стандартного вида произведение многочленов 2x 2 – 3х + 1 и 5x + 4.

(2х 2 – 3х + 1)(5х + 4) = 10х 3 + 8х 2 – 15х 2 – 12х + 5х + 4 = 10х 3 – 7х 2 – 7х + 4.

Старшие коэффициенты многочленов–множителей равны 2 и 5, а старший коэффициент произведения равен 10. Свободные члены многочленов–множителей равны 1 и 4, а свободный член произведения многочленов равен 4. Легко видеть, что старший коэффициент произведения многочленов равен произведению старших коэффициентов множителей. Аналогично, свободный член произведения многочленов равен произведению свободных членов многочленов–множителей.

Пример 3. Упростим выражение (3х – 4)(2х + 1) – (х – 2)(6х + 3).
Умножим многочлен 3х – 4 на многочлен 2х + 1, а многочлен х – 2 – на многочлен 6х + 3 и вычтем из первого произведения второе:
(3х – 4)(2х + 1) – (х – 2)(6х + 3) = (6х 2 – 8х + 3х – 4) – (6х 2 + 3х – 12х – 6) =
= 6х 2 – 8х + 3х – 4 – 6х 2 – 3х + 12х + 6 = 4х + 2.

Это конспект по математике на тему «Произведение многочленов». Выберите дальнейшие действия:

Источник

Умножение многочлена на многочлен

Урок 28. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Умножение многочлена на многочлен»

· повторить правило умножения одночлена на многочлен;

· показать правило умножения многочлена на многочлен.

На одном из предыдущих уроков мы говорили об умножении одночлен на многочлен.

На этом уроке мы научимся умножать многочлен на многочлен.

Итак, возьмём два многочлена:

Составим их произведение

тогда выражение примет вид

Теперь воспользуемся правилом умножения одночлена на многочлен, которое мы повторили в начале урока, и получим

Далее вернёмся к замене,

Снова воспользуемся правилом умножения одночлена на многочлен и получим

Таким образом, мы представили произведение многочленов в виде суммы.

Обратите внимание, что полученный в результате многочлен представляет собой сумму одночленов, которые получаются при умножении каждого слагаемого многочлена (a + b) на каждое слагаемое многочлена (c + d).

Следовательно, для того, чтобы умножить многочлен на многочлен, надо:

1. каждый член одного многочлена умножить на каждый член другого многочлена;

2. полученные произведения сложить.

Произведение многочлена на многочлен является многочленом.

При этом обратите внимание, что при умножении многочлена на многочлен до приведения подобных слагаемых у нас всегда должно получаться количество слагаемых, равное произведению числа слагаемых первого и второго многочленов.

Источник