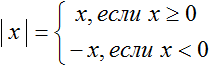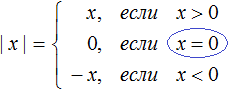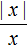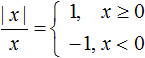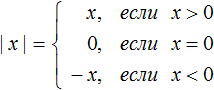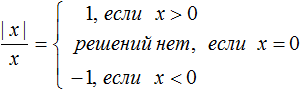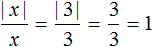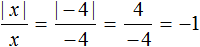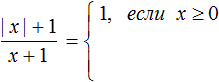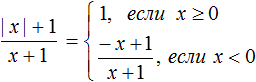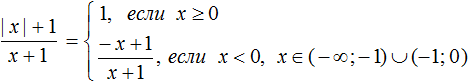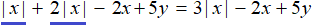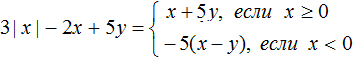что значит значение по модулю

Модуль числа

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

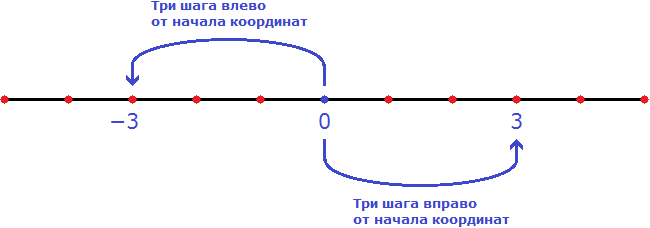
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Записывайся на занятия по математике для учеников с 1 по 11 классы.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

Оно равно a при а > 0 и −а, при а

Модуль комплексного числа

Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:

Свойства модуля комплексных чисел

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

Модуль вещественных чисел

Модуль противоположного числа, нуля, отрицательного и положительного чисел

Закрепим свойства модуля числа, которые мы рассмотрели выше:

Источник

Модуль числа — теория и решение задач

Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂

А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.

Ситуация первая

В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.

Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.

Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.

Ситуация вторая

Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.

И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?

Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.

Ситуация третья

В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.

А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.

Ну вот, ты уже почти все знаешь. Давай теперь подробнее…

Источник

Обобщённое понятие модуля числа

В данном уроке мы рассмотрим понятие модуля числа более подробно.

Что такое модуль?

Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3

Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:

Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:

Где x₁ и x₂ — числа на координатной прямой.

Например, отметим на координатной прямой числа 2 и 5.

Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:

Видим, что расстояние от числа 2 до числа 5 равно трём шагам:

Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3

То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:

Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:

Это равенство можно прочитать так: Расстояние от x₁ до x₂ равно расстоянию от x₂ до x₁.

Раскрытие модуля

Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.

Правило раскрытия модуля выглядит так:

В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.

Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x

Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5

В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0

Поэтому используем первую формулу. А именно | x | = x. Получаем | 5 | = 5.

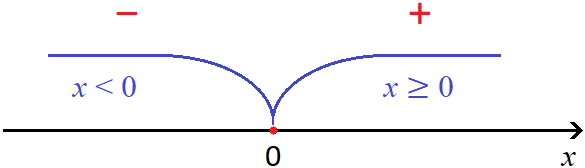
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:

А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:

Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,

Корень из числа 4 равен 2. Тогда модуль примет вид

x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x |√4 − 6| = |2 − 6| = |−4| = −(−4) = 4

На практике обычно рассуждают так:

«Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля».

Примеры:

|2| = 2 — модуль раскрылся со знаком плюс, поскольку 2 ≥ 0

Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:

В данном случае выполняется условие x=0, ведь 0 = 0

Пример 5. Раскрыть модуль в выражении |x|+ 3

Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.

Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:

Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 |x| + 3 = 3 − x = 3 − (−6) = 9

Пример 6. Раскрыть модуль в выражении x +|x + 3|

Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11

Найдём значение выражения x +|x + 3| при x=−3.

Пример 3. Раскрыть модуль в выражении

Как и прежде используем правило раскрытия модуля:

В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0

Перепишем решение так:

Пример 4. Раскрыть модуль в выражении

Но надо учитывать, что при x = − 1 знаменатель выражения 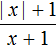обращается в ноль. Поэтому второе условие x следует дополнить записью о том, какие значения может принимать x

Преобразование выражений с модулями

Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.

Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.

Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.

Решение

Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:

В итоге имеем следующее решение:

Пример 2. Раскрыть модуль в выражении: −|x|

Решение

Источник

Абсолютная величина. Модуль.

Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).

Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.

Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:

Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:

Абсолютные величины, виды:

Свойства модуля.

.

Так как частное = , то . В силу предыдущего свойства имеем . Воспользуемся равенством , которое справедливо в силу определения модуля числа.

Основные свойства абсолютной величины.

Вещественные числа.

Комплексные числа.

Алгебраические свойства абсолютной величины.

Для каждого имеют место следующие соотношения:

Как для вещественных, так и для комплексных a, b имеют место соотношения:

Источник

Операции по модулю

Математические термины

Во всём последующем материале никак не фигурирует понятие “модуль числа” в привычном смысле (\(\lvert x \rvert\)). Речь идёт о “сравнении по модулю”. Если вы не знакомы с этим понятием, вкратце сравнение по модулю выглядит следующим образом:

Это читается “\(a\) сравнимо с \(b\) по модулю \(m\)”, и в привычных для информатики терминах обозначает следующее:

\[a \bmod m = b \bmod m,\]

Поле по модулю

Можно сказать, что в таких задачах мы оперируем не числами, а их остатками от деления на 1000000007. Это возможно благодаря следующим свойствам вычислений с остатком:

Доказательство возможности сложения, вычитания и умножения по модулю

Для начала докажем достаточно очевидное утверждение:

\[\forall n \in \mathbb: x \bmod m = (x + nm) \bmod m.\]

Значит, по определению сравнимости, \(\forall n \in \mathbb: x \equiv x + nm \pmod\), что и требовалось доказать.

\[(a + b) \bmod m = \\ = (xm + a \bmod m + ym + b \bmod m) \bmod m = \\ = (a \bmod m + b \bmod m + m(x + y)) \bmod m, = \\ = (a \bmod m + b \bmod m) \bmod m,\]

что и требовалось доказать.

Вычитание и умножение доказываются похожим образом:

Пример: вычисление факториала по модулю

В качестве примера, вычислим значение \(10^8!\) по модулю \(10^9 + 7\):

Как видите, на практике вычисления в поле по модулю отличаются от обычных лишь наличием взятия всех промежуточных результатов по модулю (строка 8). Однако существует два момента, которые нужно всегда учитывать для избежания ошибок:

Возведение в степень по модулю. Бинарное возведение в степень

Возможность умножения по модулю позволяет нам естественным образом возводить числа в различные степени по модулю. При операциях в поле по модулю степени часто сильно превышают привычные значения, и тривиальный алгоритм с линейным временем работы оказывается неприменимым. В таких ситуациях чаще всего используется алгоритм бинарного возведения в степень.

Алгоритм бинарного возведения в степень достаточно лаконичен. Его идея заключается в том, чтобы использовать возведение в квадрат промежуточных результатов, когда это возможно. Используется следующее очевидное свойство:

Таким образом засчёт одной операции умножения можно уменьшить степень вдвое. Если же текущая степень нечётная, то можно просто уменьшить её на единицу простым умножением, и получить чётную.

Простой рекурсивный вариант на C++:

Можно заметить, что в худшем случае на каждом втором вызове функции степень будет уменьшаться вдвое. Значит, время работы алгоритма можно оценить как \(O(\log p)\).

Разумеется, бинарное возведение в степень можно использовать и без модуля, но степени в таких случаях слишком малы, чтобы заметить разницу в скорости.

Деление в поле по модулю

К сожалению, деление не так легко адаптируется к полю по модулю, как другие арифметические операции. В этом разделе описывается один из способов деления по модулю, но не приводится его доказательство, так как оно значительно усложнило бы эту лекцию.

Деление по модулю определяется через умножение следующим образом:

Ключевую роль играет значение \(b^<-1>\), называющееся обратный элемент в поле по модулю. Оно никак не связано с классическим понятием обратного числа, хотя бы тем, что всегда является целым (так как в поле по модулю существуют только целые числа). Для обратного элемента должно выполняться следующее условие:

Например, обратным элементов в поле по модулю \(1000000007\) для числа \(2\) является число \(500000004\), так как \((2 * 500000004) \bmod 1000000007 = 1\). Следовательно, в поле по модулю \(1000000007\) делению на \(2\) соответствует умножение на \(500000004\)

Алгоритм нахождения обратного элемента в поле по простому модулю достаточно прост (в реализации) и выражается следующей формулой:

Как можно заметить, число \(x\) возводится в достаточно большую степень, и линейный алгоритм в этой ситуации не подойдёт. Вот и пример необходимости использования бинарного возведения в степень по модулю.

Стоит заметить что из-за использования бинарного возведения в степень, деление по модулю имеет сложность \(O(\log m)\), тогда как все остальные арифметические операции по модулю работают за \(O(1)\).

Источник