Докажите что прямые содержащие высоты треугольника пересекаются в одной точке 8 класс

Теорема о пересечении высот треугольника

Теорема

Доказательство

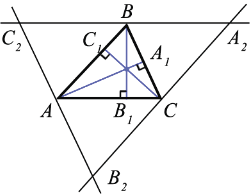
Доказать: АА₁, ВВ₁ и СС₁ пересекаются в одной точке.

Доказательство:

Проведём через каждую вершину АВС прямую, параллельную противоположной стороне.

Получим А₂В₂С₂. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А₂С и АВ = СВ₂ как противоположные стороны параллелограммов АВА₂С и АВСВ₂, поэтому А₂С = СВ₂. Аналогично С₂А = АВ₂ и С₂В = ВА₂. Кроме того, как следует из построения, СС₁А₂В₂, АА₁В₂С₂ и ВВ₁А₂С₂. Таким образом, прямые АА₁, ВВ₁ и СС₁ являются серединными перпендикулярами к сторонам треугольника А₂В₂С₂. Следовательно, они пересекаются в одной точке. Теорема доказана.

Замечательные точки треугольника : точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).

Поделись с друзьями в социальных сетях:

Источник

Докажите, что прямые, содержащие высоты треугольника, пересекаются в одной точке.

Через вершины данного треугольника провёдем прямые, параллельные противолежащим сторонам. Рассмотрим треугольник с вершинами в точках пересечения проведённых прямых. Высоты исходного треугольника лежат на серединных перпендикулярах построенного. Поэтому они пересекаются в одной точке.

Если треугольник остроугольный, то его высоты лежат на биссектрисах треугольника с вершинами в основаниях высот данного (ортотреугольник), и поэтому пересекаются в одной точке.

Если же треугольник тупоугольный, то одна его высота лежит на биссектрисе одного из углов ортотреугольника, а две другие — на биссектрисах внешних углов ортотреугольника.

Для прямоугольного треугольника утверждение очевидно.

Если треугольник остроугольный, то его высоты лежат на биссектрисах треугольника с вершинами в точках пересечения с описанной окружностью продолжений высот данного треугольника.

Пусть AA₁, BB₁, CC₁ — высоты треугольника ABC. Обозначим через , , углы треугольника ABC. Тогда из прямоугольного треугольника AB₁B находим, что

AB₁ = AB| cos|.

AС₁ = AС| cos|, BA₁ = AB| cos|, BC₁ = BC| cos|,

CA₁ = CA| cos|, CB₁ = CB| cos|.

(Если треугольник остроугольный, то знаки модуля можно опустить). Поэтому

. . =

= = 1.

Тогда по теореме Чевы прямые AA₁, BB₁ и CC₁ пересекаются в одной точке.

Пусть H — точка пересечения высот BB₁ и CC₁ треугольника ABC. Тогда

Сложив почленно эти равенства, получим, что

Следовательно, прямая AH перпендикулярна стороне BC.

Пусть O — центр описанной окружности треугольника ABC. Рассмотрим вектор = + + . Если

+ = ,

то K — вершина ромба AOBK. Значит, OK AB. Если

= + ,

то CHOK. Значит, CH AB. Поэтому точка H лежит на прямой, содержащей высоту треугольника ABC, проведённую из вершины C.

Аналогично докажем, что точка H (конец вектора ) лежит на прямых, содержащих две другие высоты треугольника. Следовательно, все три прямые пересекаются в точке H.

Воспользуемся следующим утверждением. Если A, B, C и H — произвольные точки плоскости, то

. + . + . = 0.

Пусть прямые, содержащие высоты треугольника ABC, проведённые из вершин A и B, пересекаются в точке H. Тогда AH BC и BH AC, поэтому

. = 0, . = 0.

Из приведённого выше утверждения следует, что

. = 0.

Значит, CH AB, т.е. прямая, содержащая высоту, проведённую из вершины C, также проходит через точку H.

Другие доказательства: см. МШ, N1, 1988, с.72, В.В.Прасолов, «Несколько доказательств теоремы о высотах треугольника».

Источник

Теорема о пересечении высот треугольника

Мы доказали, что биссектрисы треугольника пересекаются в одной точке, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Ранее было доказано, что медианы треугольника пересекаются в одной точке (п. 64). Оказывается, аналогичным свойством обладают и высоты треугольника.

Высоты треугольника (или их продолжения) пересекаются в одной точке.

Рассмотрим произвольный треугольник АВС и докажем, что прямые АА₁ ВВ₁ и СС₁ содержащие его высоты, пересекаются в одной точке (рис. 229).

Проведём через каждую вершину треугольника АВС прямую, параллельную противоположной стороне. Получим треугольник А₂В₂С₂. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А₂С и АВ = СВ₂ как противоположные стороны параллелограммов АВА₂С и АВСВ₂, поэтому А₂С = СВ₂. Аналогично С₂А = АВ₂ и С₂В = ВА₂. Кроме того, как следует из построения, СС₁ ⊥ А₂В₂, АА₁ ⊥ В₂С₂ и ВВ₁ ⊥ А₂С₂. Таким образом, прямые АА₁, ВВ₁ и СС₁ являются серединными перпендикулярами к сторонам треугольника А₂В₂С₂. Следовательно, оНи пересекаются в одной точке. Теорема доказана.

Итак, с каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.

Источник

Докажите что прямые содержащие высоты треугольника пересекаются в одной точке 8 класс

дПЛБЦЙФЕ, ЮФП РТСНЩЕ, УПДЕТЦБЭЙЕ ЧЩУПФЩ ФТЕХЗПМШОЙЛБ, РЕТЕУЕЛБАФУС Ч ПДОПК ФПЮЛЕ.

рПДУЛБЪЛБ

тБУУНПФТЙФЕ ФТЕХЗПМШОЙЛ, ПВТБЪПЧБООЩК РТСНЩНЙ, РТПЧЕДЈООЩНЙ ЮЕТЕЪ ЧЕТЫЙОЩ ДБООПЗП РБТБММЕМШОП РТПФЙЧПМЕЦБЭЙН УФПТПОБН.

тЕЫЕОЙЕ

юЕТЕЪ ЧЕТЫЙОЩ ДБООПЗП ФТЕХЗПМШОЙЛБ РТПЧЈДЕН РТСНЩЕ, РБТБММЕМШОЩЕ РТПФЙЧПМЕЦБЭЙН УФПТПОБН. тБУУНПФТЙН ФТЕХЗПМШОЙЛ У ЧЕТЫЙОБНЙ Ч ФПЮЛБИ РЕТЕУЕЮЕОЙС РТПЧЕДЈООЩИ РТСНЩИ. чЩУПФЩ ЙУИПДОПЗП ФТЕХЗПМШОЙЛБ МЕЦБФ ОБ УЕТЕДЙООЩИ РЕТРЕОДЙЛХМСТБИ РПУФТПЕООПЗП. рПЬФПНХ ПОЙ РЕТЕУЕЛБАФУС Ч ПДОПК ФПЮЛЕ.

еУМЙ ФТЕХЗПМШОЙЛ ПУФТПХЗПМШОЩК, ФП ЕЗП ЧЩУПФЩ МЕЦБФ ОБ ВЙУУЕЛФТЙУБИ ФТЕХЗПМШОЙЛБ У ЧЕТЫЙОБНЙ Ч ПУОПЧБОЙСИ ЧЩУПФ ДБООПЗП (ПТФПФТЕХЗПМШОЙЛ), Й РПЬФПНХ РЕТЕУЕЛБАФУС Ч ПДОПК ФПЮЛЕ.

еУМЙ ЦЕ ФТЕХЗПМШОЙЛ ФХРПХЗПМШОЩК, ФП ПДОБ ЕЗП ЧЩУПФБ МЕЦЙФ ОБ ВЙУУЕЛФТЙУЕ ПДОПЗП ЙЪ ХЗМПЧ ПТФПФТЕХЗПМШОЙЛБ, Б ДЧЕ ДТХЗЙЕ — ОБ ВЙУУЕЛФТЙУБИ ЧОЕЫОЙИ ХЗМПЧ ПТФПФТЕХЗПМШОЙЛБ.

дМС РТСНПХЗПМШОПЗП ФТЕХЗПМШОЙЛБ ХФЧЕТЦДЕОЙЕ ПЮЕЧЙДОП.

еУМЙ ФТЕХЗПМШОЙЛ ПУФТПХЗПМШОЩК, ФП ЕЗП ЧЩУПФЩ МЕЦБФ ОБ ВЙУУЕЛФТЙУБИ ФТЕХЗПМШОЙЛБ У ЧЕТЫЙОБНЙ Ч ФПЮЛБИ РЕТЕУЕЮЕОЙС У ПРЙУБООПК ПЛТХЦОПУФША РТПДПМЦЕОЙК ЧЩУПФ ДБООПЗП ФТЕХЗПМШОЙЛБ.

(еУМЙ ФТЕХЗПМШОЙЛ ПУФТПХЗПМШОЩК, ФП ЪОБЛЙ НПДХМС НПЦОП ПРХУФЙФШ). рПЬФПНХ

уМПЦЙЧ РПЮМЕООП ЬФЙ ТБЧЕОУФЧБ, РПМХЮЙН, ЮФП

йЪ РТЙЧЕДЈООПЗП ЧЩЫЕ ХФЧЕТЦДЕОЙС УМЕДХЕФ, ЮФП

дТХЗЙЕ ДПЛБЪБФЕМШУФЧБ: УН. ны, N1, 1988, У.72, ч.ч.рТБУПМПЧ, «оЕУЛПМШЛП ДПЛБЪБФЕМШУФЧ ФЕПТЕНЩ П ЧЩУПФБИ ФТЕХЗПМШОЙЛБ».

Источник

№3 8_б Теорема о пересечении высот треугольника

Продолжаем работать. Делаем конспект урока.

Просмотр содержимого документа
«№3 8_б Теорема о пересечении высот треугольника»

7.04.20. для 8-Б геометрия Урок № 3

Тема: Теорема о пересечении высот треугольника.

Цели: 1) Рассмотреть теорему о точке пересечения высот и следствие из неё;

2) Формировать умения применять известные знания для решения задач.

Скачиваем файл, чтобы не потерять данные

1. Организационный момент.

Записываем число. Тему урока и начинаем выполнять задания.

1. Сформулировать и доказать теоремы о свойстве биссектрисы и серединном перпендикуляре. Устно. Проговаривая доказательство, все делаем с помощью учебника.

2. Решить ПРОВЕРЯЕТСЯ.

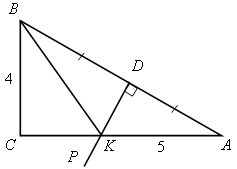
Вспоминаем свойства серединного перпендикуляра и египетский треугольник 5; 4; 3.

FK, FN серединные перпендикуляры.

Найти расстояние от точки F до стороны АВ.

Вспоминаем серединные перпендикуляры, их свойства.

Мы продолжим изучение темы «Замечательные точки треугольника» и познакомимся с теоремой о точке пересечения высот в треугольнике.

Как определяется высота в треугольнике? Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

2. Практическая работа. Выполняем в рабочей тетради. ПРОВЕРЯЕТСЯ

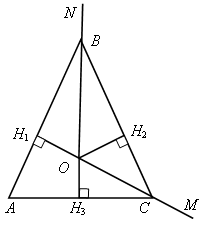
Постройте остроугольный треугольник АВС.

1. Проведите ВК  АС

2. Проведите AN  ВС.

3. Проведите CM  AB.

Все высоты пересеклись в одной точке О.

Вывод: В остроугольном треугольнике все три высоты пересеклись в одной точке. Эта точка расположена в плоскости треугольника.

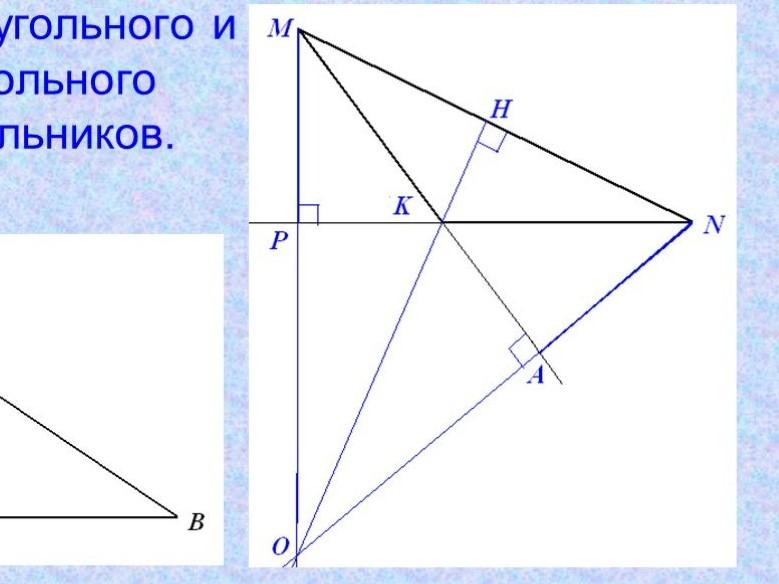
Постройте тупоугольный треугольник KMN

1. Проведите MP  NK, основание высоты лежит на продолжении NK.

2. Проведите AN  MK, основание высоты лежит на продолжении MK.

3. Проведите KH  MN.

Продолжения высот тупоугольного треугольника пересеклись в одной точке О.

Вывод: В тупоугольном треугольнике все три высоты пересеклись в одной точке. Эта точка расположена вне плоскости треугольника.

Постройте высоты в прямоугольном треугольнике (самостоятельно) и убедитесь: ПРОВЕРЯЕТСЯ

Высоты прямоугольного треугольника пересеклись в одной точке О.

В прямоугольном треугольнике все три высоты пересеклись в одной точке. Эта точка лежит в плоскости треугольника и совпадает с вершиной прямого угла треугольника.

Теорема о пересечении высот треугольника:

Высоты треугольника (или их продолжения) пересекаются в одной точке.

(доказательство смотрим в ссылках)

Закрепление изученного материала. Делаем в тетради

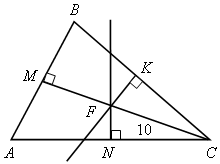
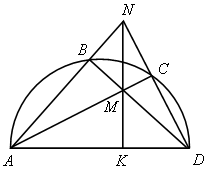
Дуга АD – полуокружность.

Доказать MN 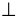АD.

1. Δ ABD: B=90˚-опирается на диаметр.

M=ACÇBDÇNKÞNK-высота ΔANDÞ MN 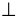АD.

1) АВО = 180° – АВN =

180°– СВN = CВО, то есть ВО – биссектриса АВС,

аналогично СО – биссектриса АСВ.

2) По теореме о биссектрисе угла, точка О

равноудалена от сторон АВ, ВС, АС. Таким образом,

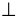
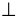
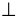
ОН₁ = ОН₂ = ОН₃, где ОН₁ АВ, ОН₂ ВС, ОН₃ АС.

2. Получили, что АВ, ВС, АС – касательные к окружности с центром в точке О и радиусом, равным ОН₁.

Домашнее задание. Рефлексия.

Мои действия на занятии (слушал, выполнял эксперимент, общался. )

Я на занятии научился, узнал.. (оценивать свои действия, приобретать знания caмостоятельно и т.д.)

В чем ценность занятия для меня?

Что вызвало затруднения и почему?

Меня порадовало (огорчило)

Стр. 184 №1– 20, вопросы. Проговорить вслух, запомнить.

Источник