в каком отношении находятся содержание и объем понятия ответ
В каком отношении находятся содержание и объем понятия ответ
мелгйс 2. рпосфйе
1. рПОСФЙЕ ЛБЛ ЖПТНБ НЩЫМЕОЙС.
тБЪМЙЮЙЕ НЕЦДХ УХЭЕУФЧЕООЩНЙ Й ОЕУХЭЕУФЧЕООЩНЙ РТЙЪОБЛБНЙ ОЕ СЧМСЕФУС УФТПЗЙН: ФП, ЮФП Ч ПДОПН ПФОПЫЕОЙЙ ЛБЦЕФУС УХЭЕУФЧЕООЩН, Ч ДТХЗЙИ ПФОПЫЕОЙСИ НПЦЕФ ПЛБЪБФШУС ОЕУХЭЕУФЧЕООЩН, Й ОБПВПТПФ.
2. мПЗЙЮЕУЛБС УФТХЛФХТБ РПОСФЙС.
мПЗЙЮЕУЛХА УФТХЛФХТХ РПОСФЙС УПУФБЧМСАФ ЕЗП УПДЕТЦБОЙЕ Й ПВЯЕН.
уПДЕТЦБОЙЕ Й ПВЯЕН Й РПОСФЙС ЧЪБЙНПУЧСЪБОЩ. ьФБ ЧЪБЙНПУЧСЪШ ЧЩТБЦБЕФУС Ч ЪБЛПОЕ ПВТБФОПЗП ПФОПЫЕОЙС НЕЦДХ ПВЯЕНПН Й УПДЕТЦБОЙЕН РПОСФЙС, ЛПФПТЩК ХУФБОБЧМЙЧБЕФ, ЮФП ХЧЕМЙЮЕОЙЕ УПДЕТЦБОЙС РПОСФЙС ЧЕДЕФ Л ХНЕОШЫЕОЙА ЕЗП ПВЯЕНБ, Й ОБПВПТПФ. оБРТЙНЕТ, ЧПЪШНЕН ДЧБ РПОСФЙС: «ЮЕМПЧЕЛ» Й «ЕЧТПРЕЕГ». уПДЕТЦБОЙЕ ЧФПТПЗП РПОСФЙС ВПЗБЮЕ, ЙВП Л РТЙЪОБЛБН ЮЕМПЧЕЛБ ЧППВЭЕ ЪДЕУШ ЕЭЕ ДПВБЧМСАФУС РТЙЪОБЛЙ, ИБТБЛФЕТЙЪХАЭЙЕ ЕЧТПРЕКГБ, ПДОБЛП РП ПВЯЕНХ ПОП ЗПТБЪДП НЕОШЫЕ РЕТЧПЗП РПОСФЙС.
3. чЙДЩ РПОСФЙК Й ПФОПЫЕОЙС НЕЦДХ ОЙНЙ.
рП ПВЯЕНХ (РП ЛПМЙЮЕУФЧХ) ЧУЕ РПОСФЙС НПЦОП ТБЪДЕМЙФШ ОБ ФТЙ ЧЙДБ:
Ч) РХУФЩЕ (ОХМЕЧЩЕ), Ч ПВЯЕН ЛПФПТЩИ ОЕ ЧИПДЙФ ОЙ ПДОПЗП ТЕБМШОП УХЭЕУФЧХАЭЕЗП РТЕДНЕФБ,- «ЛЕОФБЧТ», «ТХУБМЛБ», «ЮЕМПЧЕЛ, РПВЩЧБЧЫЙК ОБ нБТУЕ», Й Ф. Р.
рП УПДЕТЦБОЙА (РП ЛБЮЕУФЧХ) РПОСФЙС ТБЪДЕМСАФУС ОБ УМЕДХАЭЙЕ ЗТХРРЩ:
В) пФОПУЙФЕМШОЩЕ Й ВЕЪПФОПУЙФЕМШОЩЕ. пФОПУЙФЕМШОЩНЙ ОБЪЩЧБАФ ФБЛЙЕ РПОСФЙС, УПДЕТЦБОЙС ЛПФПТЩИ ЧЪБЙНОП РТЕДРПМБЗБАФ УХЭЕУФЧПЧБОЙЕ ДТХЗ ДТХЗБ, ЗТХВП ЗПЧПТС, ЬФП РПОСФЙС, УХЭЕУФЧХАЭЙЕ ФПМШЛП Ч РБТЕ. оБРТЙНЕТ, «РТБЧПЕ-МЕЧПЕ», «ЧЕТИ-ОЙЪ», «ХЮЕОЙЛ-ХЮЙФЕМШ» Й Ф. Р. рТЕДУФБЧШФЕ УЕВЕ, ЮФП Х ОБУ ПУФБМПУШ МЙЫШ РПОСФЙЕ «РТБЧПЕ», Б РПОСФЙЕ «МЕЧПЕ» ЙУЮЕЪМП. оЕФТХДОП УППВТБЪЙФШ, ЮФП, ПУФБЧЫЙУШ ПДОП, РПОСФЙЕ «РТБЧПЕ» РПФЕТСЕФ ЧУСЛЙК УНЩУМ Й ФПЦЕ ЙУЮЕЪОЕФ. фБЛЙЕ РПОСФЙС НПЗХФ УХЭЕУФЧПЧБФШ МЙЫШ Ч РБТЕ, ЙВП ЙИ УПДЕТЦБОЙС ПРТЕДЕМСАФУС ПФОПЫЕОЙЕН ДТХЗ Л ДТХЗХ. вЕЪПФОПУЙФЕМШОЩЕ РПОСФЙС ОЕ УПДЕТЦБФ УУЩМЛЙ ОБ ДТХЗЙЕ РПОСФЙС Й НПЗХФ УХЭЕУФЧПЧБФШ УБНЙ РП УЕВЕ, ОБРТЙНЕТ, «ЛБТБОДБЫ», «ПЧГБ», «ЦНЩИ».
Ч) рПМПЦЙФЕМШОЩЕ Й ПФТЙГБФЕМШОЩЕ. рПМПЦЙФЕМШОЩЕ РПОСФЙС ПФПВТБЦБАФ УЧПКУФЧБ, РТЙУХЭЙЕ РТЕДНЕФБН, ОБРТЙНЕТ, «ЧЩУПЛЙК», «БМЮОЩК», «ЦЕМБООЩК». пФТЙГБФЕМШОЩЕ РПОСФЙС ПФПВТБЦБАФ УЧПКУФЧБ, ПФУХФУФЧХАЭЙЕ Х РТЕДНЕФБ, ОБРТЙНЕТ, «ОЕЗТБНПФОЩК», «ВЕУЛПТЩУФОЩК», «ОЕЦЕМБООЩК». еУМЙ РПОСФЙЕ «ЗТБНПФОЩК» ПФПВТБЦБЕФ УЧПКУФЧП ЮЕМПЧЕЛБ ХНЕФШ ЮЙФБФШ Й РЙУБФШ, ФП РПОСФЙЕ «ОЕЗТБНПФОЩК» ЗПЧПТЙФ П ФПН, ЮФП Х ПВЯЕЛФПЧ, ЧИПДСЭЙИ Ч ЕЗП ПВЯЕН, ДБООПЕ УЧПКУФЧП ПФУХФУФЧХЕФ. уМЕДХЕФ, РТБЧДБ, ПВТБФЙФШ ЧОЙНБОЙЕ ОБ ФП, ЙОПЗДБ УМПЧБ, ЧЛМАЮБАЭЙЕ Ч УЕВС ПФТЙГБФЕМШОЩЕ ЮБУФЙГЩ «ОЕ» ЙМЙ «ВЕЪ» («ВЕУ»), ЧЩТБЦБАФ РПМПЦЙФЕМШОЩЕ РПОСФЙС, Ф. Е. ПФПВТБЦБАФ ОЕЛПФПТЩЕ РТЙУХЭЙЕ РТЕДНЕФБН УЧПКУФЧБ: «ОЕОБЧЙУФШ», «ОЕТСИБ», «ВЕУРЕЮОЩК» Й Ф. Р.
З) уПВЙТБФЕМШОЩЕ Й ОЕУПВЙТБФЕМШОЩЕ (ТБЪДЕМЙФЕМШОЩЕ). ч УПВЙТБФЕМШОЩИ РПОСФЙСИ ОЕЛПФПТПЕ НОПЦЕУФЧП, УПУФПСЭЕЕ ЙЪ ПДОПТПДОЩИ РТЕДНЕФПЧ, НЩУМЙФУС ЛБЛ ЕДЙОПЕ ГЕМПЕ, ОБРТЙНЕТ, «УФБДП», «ЖМПФ», «МЕУ», «УПЪЧЕЪДЙЕ» Й Ф. Р. ьФБ ГЕМПУФОПУФШ РТПСЧМСЕФУС Ч ФПН, ЮФП НОПЗЙЕ УЧПКУФЧБ УПЧПЛХРОПУФЙ РТЕДНЕФПЧ РТЙОБДМЕЦБФ ЕК ЛБЛ ГЕМПНХ, ОП ОЕ РТЙОБДМЕЦБФ УПУФБЧМСАЭЙН ЕЕ РТЕДНЕФБН. нПЦОП УЛБЪБФШ, ОБРТЙНЕТ, «ч МЕУХ МЕЗЛП ЪБВМХДЙФШУС» ЙМЙ «дБООПЕ УПЪЧЕЪДЙЕ РПИПЦЕ ОБ НЕДЧЕДЙГХ», ОП ЬФПЗП ОЕМШЪС УЛБЪБФШ ПВ ПФДЕМШОПН ДЕТЕЧЕ ЙМЙ ЪЧЕЪДЕ. уПЧПЛХРОПУФШ РТЕДНЕФПЧ ЮБУФП РТЙПВТЕФБЕФ УЧПКУФЧБ, ЛПФПТЩЕ МЙЫЕОЩ ЧИПДСЭЙЕ Ч ОЕЕ РТЕДНЕФЩ.
дЕМЕОЙЕ РПОСФЙК ОБ РПМПЦЙФЕМШОЩЕ Й ПФТЙГБФЕМШОЩЕ, ПФОПУЙФЕМШОЩЕ Й ВЕЪПФОПУЙФЕМШОЩЕ ОЕ СЧМСЕФУС ЦЕУФЛЙН. ч ЪБЧЙУЙНПУФЙ ПФ ФПЗП ЛБЛ НЩ ЖПТНХМЙТХЕН УПДЕТЦБОЙЕ НПЦЕФ НЕОСФШУС Й ОБЫБ ПГЕОЛБ РПОСФЙС.
пФОПЫЕОЙС НЕЦДХ РПОСФЙСНЙ:
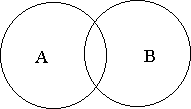
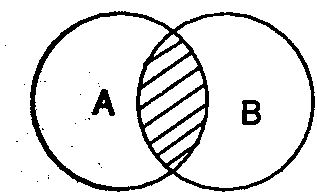
2) ретеуеюеойе. ч ПФОПЫЕОЙЙ РЕТЕУЕЮЕОЙС ОБИПДСФУС РПОСФЙС, ПВЯЕНЩ ЛПФПТЩИ УПЧРБДБАФ МЙЫШ ЮБУФЙЮОП.
уФХДЕОФ (б)
уРПТФУНЕО (ч)
уХЭЕУФЧХАФ УРПТФУНЕОЩ, ОЕ СЧМСАЭЙЕУС УФХДЕОФБНЙ. еУФШ УФХДЕОФЩ ОЕ ЪБОЙНБАЭЙЕУС УРПТФПН, ОП ЙНЕАФУС УРПТФУНЕОЩ ПДОПЧТЕНЕООП СЧМСАЭЙЕУС УФХДЕОФБНЙ
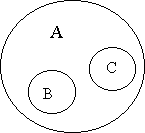
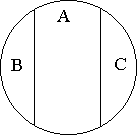
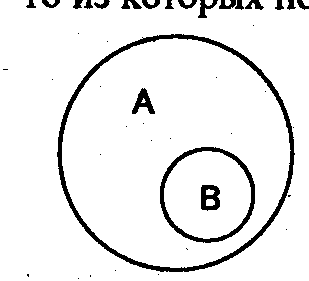
1) упрпдюйоеойе. ч ПФОПЫЕОЙЙ УПРПДЮЙОЕОЙС ОБИПДСФУС ДЧБ ЙМЙ ВПМЕЕ ОЕРЕТЕУЕЛБАЭЙИУС РПОСФЙК, РТЙОБДМЕЦБЭЙИ ПВЭЕНХ ТПДПЧПНХ РПОСФЙА.
дЕТЕЧШС (б)
уПУОБ (ч)
вЕТЕЪБ (у)
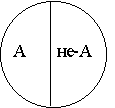
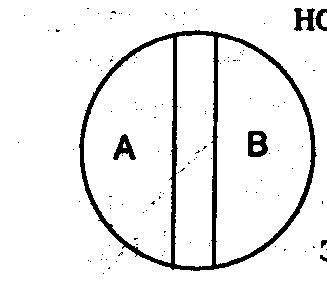
2) ртпфйчпрпмпцопуфш. ч ПФОПЫЕОЙЙ РТПФЙЧПРПМПЦОПУФЙ ОБИПДСФУС РПОСФЙС, ЛПФПТЩЕ СЧМСАФУС ЧЙДБНЙ ПДОПЗП Й ФПЗП ЦЕ ТПДБ, РТЙ ЬФПН ПДОП ЙЪ ОЙИ УПДЕТЦЙФ ЛБЛЙЕ-ФП РТЙЪОБЛЙ, Б ДТХЗПЕ ЬФЙ РТЙЪОБЛЙ ПФТЙГБЕФ Й ЪБНЕОСЕФ РТПФЙЧПРПМПЦОЩНЙ РТЙЪОБЛБНЙ (ПВЯЕНЩ РПОСФЙК б Й ч Ч ПВЯЕНЕ ТПДПЧПЗП РПОСФЙС ЪБОЙНБАФ ОБЙВПМЕЕ ХДБМЕООЩЕ ЮБУФЙ).
гЧЕФ (б)
юЕТОЩК (ч)
вЕМЩК (у)
ч УХННЕ ПВЯЕНЩ РТПФЙЧПРПМПЦОЩИ РПОСФЙК ОЕ ЙУЮЕТРЩЧБАФ ПВЯЕН ТПДПЧПЗП РПОСФЙС. ьФЙ РПОСФЙС НПЦОП ТБУУНБФТЙЧБФШ ЛБЛ УПРПДЮЙОЕООЩЕ.
Логика.
13. Содержание и объем понятий.
Любое понятие имеет содержание и объем.
Содержанием понятия является совокупность характеризующих его предмет существенных признаков, подразумевающихся в данном понятии.
Объем понятия составляет совокупность или множество предметов, которое мыслится в понятии.
Любое понятие может быть полно охарактеризовано при помощи определения его содержания (иными словами – смысла) и установления предметов, с которыми данное понятие имеет определенные связи.
Независимо от сознания человека в окружающем мире существуют различные предметы. Эти предметы характеризуются множеством. Множество может быть конечным или бесконечным. Если количество предметов, входящих в множество, поддается исчислению, множество считается конечным. Если такие предметы не поддаются исчислению, множество называют бесконечным. Необходимо упомянуть об отношениях включения, принадлежности и тождества.
Отношение включения – это отношение вида и рода. Множество А является частью или подмножеством множества В, если каждый элемент А есть элемент В. Отражается в виде формулы А є В (множество А входит в множество В). В отношении принадлежности класса принадлежит классу А и записывается как а є А. Отношение тождества подразумевает, что множества А и В совпадают. Это закрепляется как А є В.
Содержание понятия называется его интенсиональностью, а его отношение к каким-либо объектам – экстенсиональностью.
Интенсиональность понятий. Чаще всего в процессе толкования термина «содержание понятия» его определяют в качестве понятия как такового. В этом случае подразумевается, что содержание понятия есть система признаков, при посредстве которых предметы, содержащиеся в понятии, обобщаются и выделяются из массы других.
Из сказанного выше видно, что содержанием понятия является некая информация, содержащая сведения о предметах, явлениях, процессах, входящих в данное понятие.
Например, слова «книга» – «книжонка»; «бабка» – «бабушка» – «бабуля» вполне иллюстрируют коннотацию.
Экстенсиональность понятий. Любое понятие отражает какой-либо предмет, содержит признаки, характеризующие и отделяющие его от других предметов. Этот предмет всегда связан с другими предметами, которые не входят в содержание данного понятия, однако имеют признаки, частично повторяющие признаки предмета, отраженного в понятии. Эти предметы составляют особую группу. Такую группу можно определить как совокупность объектов, характеризующихся наличием общих признаков, закрепленных хотя бы одним понятием.
Объем и содержание понятия. Отношения между понятиями



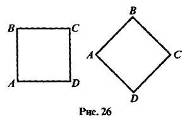
Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали. Можно указать и другие его свойства.
Среди свойств объекта различают существенные и несущественные. Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать. Например, для квадрата существенными являются все свойства, названные выше. Несущественно для квадрата ABCD свойство «сторона AD горизонтальна». Если квадрат повернуть, то сторона AD окажется расположенной по-другому (рис. 26).
Поэтому, чтобы понимать, что представляет собой данный математический объект, надо знать его существенные свойства.
Когда говорят о математическом понятии, то обычно имеют в виду множество объектов, обозначаемых одним термином (словом или группой слов). Так, говоря о квадрате, имеют в виду все геометрические фигуры, являющиеся квадратами. Считают, что множество всех квадратов составляет объем понятия «квадрат».
Любое понятие имеет не только объем, но и содержание.
Содержание понятия- это множество всех существенных свойств объекта, отраженных в этом понятии.
Рассмотрим, например, понятие «прямоугольник».
Между объемом понятия и его содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Так, например, объем понятия «квадрат» является частью объема понятия «прямоугольник», а в содержании понятия «квадрат» содержится больше свойств, чем в содержании понятия «прямоугольник» («все стороны равны», «диагонали взаимно перпендикулярны» и др.).
Любое понятие нельзя усвоить, не осознав его взаимосвязи с другими понятиями. Поэтому важно знать, в каких отношениях могут находиться понятия, и уметь устанавливать эти связи.
Отношения между понятиями тесно связаны с отношениями между их объемами, т.е. множествами.
Условимся понятия обозначать строчными буквами латинского алфавита: а, b, с. z.
Пусть заданы два понятия а и b. Объемы их обозначим соответственно А и В.
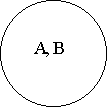
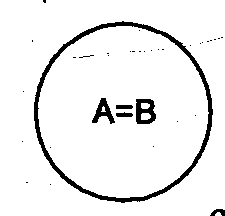
Если А = В, то говорят, что понятия а и b тождественны.
Например, тождественны понятия «равносторонний треугольник» и «равноугольный треугольник», так как их объемы совпадают.
Если множества А и В не связаны отношением включения, то говорят, что понятия а и b не находятся в отношении рода и вида и не тождественны. Например, не связаны такими отношениями понятия «треугольник» и «прямоугольник».
Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник». Среди них можно указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие «параллелограмм».
В-третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику.
Установим, например, отношения между следующими парами понятий а и Ь, если:
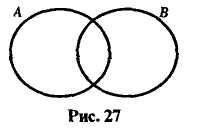
В случае 1) объемы понятий пересекаются, но не одно множество не является подмножеством другого (рис. 27).
Следовательно, можно утверждать, что данные понятия а и b не находятся в отношении рода и вида.
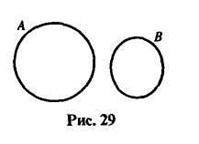
В случае 3) объемы понятий не пересекаются, так как ни про один отрезок нельзя сказать, что он является прямой, и ни одна прямая не может быть названа отрезком (рис. 29).
Следовательно, данные понятия не находятся в отношении рода и вида.
О понятиях «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок- часть прямой, а не ее вид. И если видовое понятие обладает всеми свойствами родового понятия, то часть не обязательно обладает всеми свойствами целого. Например, отрезок не обладает таким свойством прямой, как ее бесконечность.
В каком отношении находятся содержание и объем понятия ответ
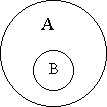
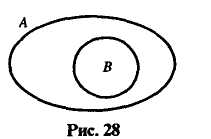
3 – подчинение. В отношении подчинения (субординации) находятся понятия, если объем одного полностью входит в объем другого, но не исчерпывает его. Это отношение вида – В и рода – А (млекопитающее и кошка).
Несовместимыми называются понятия, объемы которых не совпадают. Несовместимые понятия могут находиться между собой в следующих отношениях.
1 – соподчинение. В отношении соподчинения (координации) находятся понятия, объемы которых исключают друг друга, но принадлежат некоторому более общему родовому понятию. Напр., «ель» – B, «береза» – C принадлежат объему понятия «дерево» – А. Они изображаются неперекрещивающимися кругами внутри общего круга. Это виды одного и того же рода.
2 – противоположность. В отношении противоположности (контрарности) находятся два понятия, признаки которых противоречат друг другу, а сумма их объемов не исчерпывает родового понятия (храбрость – трусость).
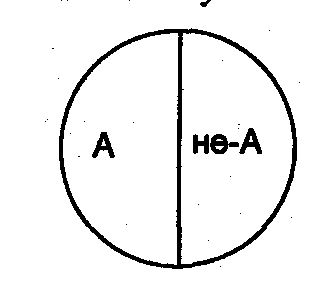
3 – противоречие. В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя никакими другими (напр., А – белая краска, тогда понятие, находящееся с ним в отношениях противоречия, следует обозначить не-А (не белая краска). Круг Эйлера в этом случае делится пополам и между ними нет никакого третьего понятия.
14. ЛОГИЧЕСКАЯ ОПЕРАЦИЯ ОБОБЩЕНИЯ И ОГРАНИЧЕНИЯ ПОНЯТИЙ
Большое значение для достижения определенности нашего мышления имеют логические операции обобщения и ограничения понятий, основанные на законе обратного отношения между содержанием и объемом понятия.
Обобщить понятие – значит перейти от понятия с меньшим объемом, но большим содержанием к понятию с большим объемом, но меньшим содержанием. Напр., обобщая понятие «городской суд», мы получим понятие «суд», объем нового понятия шире исходного, т. к. первое относится ко второму как вид к роду. Вместе с тем содержание нового понятия уменьшилось, поскольку мы исключили его видовые признаки. Обобщение понятия может быть многоступенчатым, напр. «уголовное преступление», «преступление», «противоправное деяние», «деяние». Однако обобщение понятий не может быть бесконечным. Пределом обобщения являются категории – понятия, обладающие предельно широким объемом: материя, сознание, движение, свойство и др. Категории не имеют родового понятия.
Ограничение понятия представляет собой операцию, противоположную обобщению. Ограничить понятие – значит перейти от понятия с большим объемом, но меньшим содержанием к понятию с меньшим объемом, но большим содержанием. Напр., «юрист», «следователь», «следователь прокуратуры», «следователь прокуратуры Петров». Пределом ограничения понятия является единичное понятие.
Логические операции обобщения и ограничения понятий широко применяются в практике мышления: переходя от понятия одного объема к понятию другого объема, мы уточняем предмет нашей мысли, делаем наше мышление более определенным и последовательным.
Обобщение и ограничение понятий нельзя смешивать с мысленным переходом от части к целому и выделением части из целого. Напр., сутки делятся на часы, часы на минуты, минуты на секунды. Каждое последующее понятие не является видом предыдущего, которое в свою очередь нельзя рассматривать как родовое. Поэтому переход от понятия «час» к понятию «сутки» является не обобщением, а переходом от части к целому.
15. ВИДЫ ОПРЕДЕЛЕНИЙ
По функциям, которые определения выполняют в процессе познания, они делятся на номинальные и реальные.
Номинальным (от лат. nomen – имя) называется определение, посредством которого вводится новое имя, оно как бы выражает требование называть данным термином определенный предмет. Напр., «Термин «юридический» означает относящийся к правоведению, правовой». Такое определение может быть охарактеризовано с точки зрения эффективности, целесообразности.
Реальным называется определение, раскрывающее существенные признаки предмета, описывающее какой-либо объект. Напр., «улика – это доказательство виновности обвиняемого в совершенном преступлении». Реальные определения должны верно отражать предмет, их можно характеризовать с точки зрения истинности.
§ 5. Логические отношения между понятиями
§ 5. Логические отношения между понятиями
Так как все предметы находятся во взаимодействии и взаимообусловленности, то и понятия, отражающие данные предметы, также находятся в определенных отношениях. Конкретные виды отношений устанавливаются в зависимости от содержания и объема понятий, которые сравниваются.
Если понятия не имеют общих признаков, далеки друг от друга по своему содержанию, то они называются несравнимыми. Например, «симфоническая музыка» и «кассационная жалоба», «процессуальные акты предварительного расследования» и «общая тетрадь».
Сравнимыми называются понятия, отражающие некоторые общие существенные признаки предмета или класса однородных предметов. Например, «юрист» и «адвокат», «взятка» и «кража».
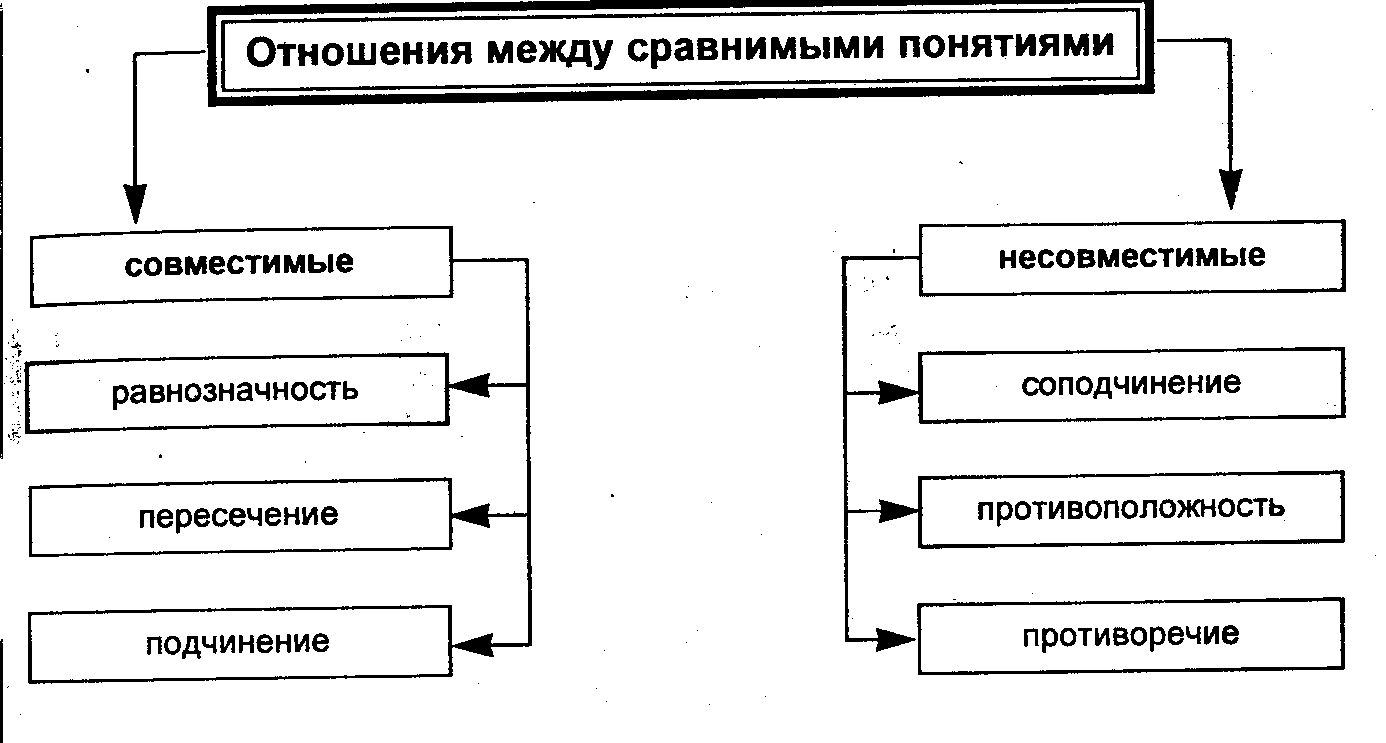
В логических отношениях могут находиться только сравнимые понятия. В зависимости от того, как соотносятся их объемы, понятия делятся на две группы: совместимые и несовместимые.
Рассмотрим совместимые понятия.
В отношениях равнозначности находятся совместимые понятия, объемы которых полностью совпадают. В таких понятиях мыслится один и тот же предмет или класс однородных предметов. Однако содержание этих понятий различно, так как каждое из них отражает только определенную сторону (существенный признак) данного предмета или класса однородных предметов.
Необходимо отличать равнозначные понятия от равнозначных слов-синонимов. У равнозначных понятий одинаковый объем, но разное содержание. А слова-синонимы выражают понятия с одинаковым объемом и содержанием. Замена в любом осмысленном высказывании слов-синонимов друг с другом не влияет на смысл высказывания. Замена же слов, выражающих равнозначные понятия, может привести к существенному искажению смысла. Например, в высказывании «В 1980 году Москва была столицей игр XXII Олимпиады» нельзя заменить понятие «столица игр XXII Олимпиады» равнозначным ему понятием «центр Московской области». Таким образом, слова или словосочетания, выражающие равнозначные понятия, сами по себе не являются равнозначными.
В отношении пересечения находятся совместимые понятия, у которых объемы частично совпадают. Частично совпадает и содержание данных понятий.
В отношении подчинения находятся совместимые понятия, объем одного из которых полностью входит в объем другого, составляя его часть.
Объем первого понятия шире объема второго понятия: кроме кражи личного имущества граждан в него входит также кража государственного, кооперативного имущества.
Из двух понятий, находящихся в отношении подчинения, понятие с большим объемом (подчиняющее) является родовым, или родом по отношению к понятию с меньшим объемом (подчиненному), а последнее по отношению к первому называется видовым, или видом. Родовидовые отношения лежат в основе логических операций ограничения и обобщения понятий, деления объема понятий и некоторых видов определения.
Перейдем к рассмотрению несовместимых понятий.
При иллюстрации отношений между несовместимыми понятиями возникает потребность во введении более широкого по объему понятия, которое включало бы объемы несовместимых понятий.
В отношении соподчинения находятся два или более непересекающихся понятий, принадлежащих общему родовому понятию.
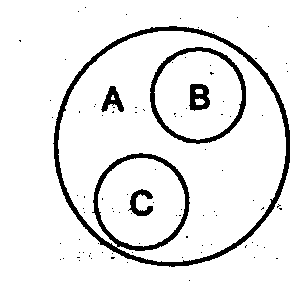
В отношении противоположности находятся понятия, которые являются видами одного и того же рода, и при этом одно из них содержит какие-то признаки, а другое эти признаки отрицает и заменяет противоположными признаками.
В отношении противоречия находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками.
Таким образом, уяснение логической структуры понятий, определение их видов и отношений между сравнимыми понятиями дает возможность перейти к рассмотрению логических действий, или операций над понятиями.
Читайте также
§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ При образовании понятий часто бывает важно не только указывать их вид, но и выяснять, в каком отношении находятся эти понятия к другим понятиям. Высказывания типа “это понятие близко такому-то понятию” только запутывают суть дела. Нужно
Логические отношения между простыми атрибутивными суждениями
Логические отношения между простыми атрибутивными суждениями Так же, как и понятия, суждения могут быть сравнимыми и несравнимыми. Мы можем рассмотреть только сравнимые суждения. Сравнимыми называются суждения с одинаковыми субъектами и предикатами и различающиеся
§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ Рассматривая отношения между понятиями, следует прежде всего различать понятия сравнимые и несравнимые.Сравнимыми называются понятия, имеющие некоторые признаки, позволяющие эти понятия сравнивать. Например, «пресса» и «телевидение» —
§ 6. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ
§ 6. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ Суждения делятся на сравнимые и несравнимые.Несравнимыми являются суждения, имеющие разные субъекты или предикаты. Таковы, например, два суждения: «Некоторые студенты первокурсники» и «Некоторые студенты
§ 4. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ
§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
§ 5. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ При образовании понятий часто бывает важно не только указывать их вид, но и выяснять, в каком отношении находятся эти понятия к другим понятиям. Высказывания типа “это понятие близко такому-то понятию” только запутывают суть дела. Нужно
Глава III. Отношения между понятиями
Глава III. Отношения между понятиями Объективные отношения между самими предметами находят свое отражение в отношениях между понятиями. Все многообразие этих отношений можно классифицировать также на основе важнейших логических характеристик понятия: его содержания и
1. Отношения между понятиями по их содержанию
1. Отношения между понятиями по их содержанию Сравнимые понятия. По содержанию могут быть два основных вида отношений между понятиями — сравнимость и несравнимость. При этом сами понятия соответственно называются «сравнимыми» и «несравнимыми».Сравнимые — это понятия,
2. Отношения между понятиями по их объему
2. Отношения между понятиями по их объему Совместимые понятия. Сравнимые понятия могут по объему также иметь два основных вида отношений — совместимость и несовместимость. А сами соотносящиеся понятия называются «совместимыми» и «несовместимыми».Совместимые — это
3. Логические отношения между теориями
3. Логические отношения между теориями Если логические отношения существуют между понятиями и между суждениями, то вправе ли мы говорить о логических отношениях между теориями? Ведь это неизмеримо более сложные мыслительные конструкции! Да, вправе и именно потому, что
Глава III. Отношения между понятиями
Глава III. Отношения между понятиями 1. Отношения между понятиями по их содержанию Сравнимые и несравнимые понятия1. Определите, какие из названных ниже пар понятий сравнимые, какие — несравнимые: «металл» — «золото», «вода» — «камень», «космос» — «ключ», «душа»—«песня»,
1. Отношения между понятиями по их содержанию
1. Отношения между понятиями по их содержанию Сравнимые и несравнимые понятия1. Определите, какие из названных ниже пар понятий сравнимые, какие — несравнимые: «металл» — «золото», «вода» — «камень», «космос» — «ключ», «душа»—«песня», «правовой нигилизм» — «соната»,
2. Отношения между понятиями по их объему
2. Отношения между понятиями по их объему 1. Какие из указанных ниже пар понятий относятся к совместимым, а какие — к несовместимым: «снег» — «дождь», «время года» — «зима», «самолет» — «вертолет», «ложка» — «вилка», «мужчина» — «женщина», «рыба» — «муравей», «учитель»
§ 1. Возможные логические отношения между суждениями
§ 1. Возможные логические отношения между суждениями Интерес логиков к структуре суждений вызван их желанием проявить все возможные формы суждений, с помощью которых суждения имплицируют друг друга. Помимо импликации суждения могут быть связаны и другими отношениями.
ЛЕКЦИЯ № 7 Отношения между понятиями
ЛЕКЦИЯ № 7 Отношения между понятиями 1. Общая характеристика отношений между понятиями Окружающий нас мир по своей природе — очень сложная система. Проявляется эта природа в том, что все предметы, которые мы только можем себе представить, всегда находятся во
Глава 4. Логические категории и отношения между понятиями
Глава 4. Логические категории и отношения между понятиями Начинается глава с перечисления десяти Аристотелевых категорий. Насколько я понял Георгия Ивановича, эти категории — это самые общие, корневые классы всех понятий. Вот, собственно, список:1. Субстанция