что значит абсолютное значение числа

Модуль числа — теория и решение задач

Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂

А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.

Ситуация первая

В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.

Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.

Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.

Ситуация вторая

Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.

И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?

Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.

Ситуация третья

В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.

А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.

Ну вот, ты уже почти все знаешь. Давай теперь подробнее…

Источник

Нельзя так просто взять и вычислить абсолютное значение

Кажется, задача вычисления абсолютного значения (или модуля) числа совершенно тривиальна. Если число отрицательно, давайте сменим знак. Иначе оставим как есть. На Java это будет выглядеть примерно так:

Вроде бы это слишком просто даже для вопроса на собеседовании на позицию джуна. Есть ли тут подводные камни?

Этот метод JIT-компилятор в идеале может вообще удалить полностью, потому что речь идёт просто про реинтерпретацию набора бит в процессоре, чтобы типы данных сошлись. А сами биты остаются одни и те же и процессору обычно наплевать на типы данных. Хотя говорят, что всё-таки это может привести к пересылке из регистра с плавающей точкой в регистр общего назначения. Но всё равно очень быстро.

Ладно, у нас осталось два ветвления для всех положительных чисел и нулей. Всё равно кажется, что много. Мы знаем, что ветвления — это плохо, если branch predictor не угадает, они могут очень дорого стоить. Можно ли сделать меньше? Оказывается, можно любой нуль превратить в положительный, если вычесть его из 0.0 :

Таким образом, можно написать:

Отлично, у нас теперь всегда одна ветка. Победа? Но как насчёт сделать всегда ноль веток? Возможно ли это?

Этот способ действительно не содержит ветвлений, и профилирование показывает, что пропускная способность метода при определённых условиях увеличивается процентов на 10%. Предыдущая реализация с одним ветвлением была в стандартной библиотеке Java с незапамятных времён, а вот в грядущей Java 18 уже закоммитили улучшенную версию.

В ряде случаев, впрочем, эти улучшения ничего не значат, потому что JIT-компилятор может использовать соответствующую ассемблерную инструкцию при её наличии и полностью проигнорировать Java-код. Например, на платформе ARM используется инструкция VABS. Так что пользы тут мало. Но всё равно интересная статья получилась!

Источник

Абсолютная величина. Модуль.

Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).

Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.

Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:

Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:

Абсолютные величины, виды:

Свойства модуля.

.

Так как частное = , то . В силу предыдущего свойства имеем . Воспользуемся равенством , которое справедливо в силу определения модуля числа.

Основные свойства абсолютной величины.

Вещественные числа.

Комплексные числа.

Алгебраические свойства абсолютной величины.

Для каждого имеют место следующие соотношения:

Как для вещественных, так и для комплексных a, b имеют место соотношения:

Источник

СОДЕРЖАНИЕ

Терминология и обозначения

Определение и свойства

Вещественные числа

Поскольку символ квадратного корня представляет собой уникальный положительный квадратный корень (в применении к положительному числу), отсюда следует, что

| Икс | знак равно Икс 2 <\ Displaystyle | х | = <\ sqrt <х ^ <2>>>>

эквивалентно определению, приведенному выше, и может использоваться как альтернативное определение абсолютного значения действительных чисел.

Ниже приведены некоторые дополнительные полезные свойства. Это либо непосредственные следствия определения, либо подразумеваются четырьмя фундаментальными свойствами, указанными выше.

Два других полезных свойства, касающихся неравенств:

Эти отношения могут использоваться для решения неравенств, касающихся абсолютных значений. Например:

Абсолютное значение, как «расстояние от нуля», используется для определения абсолютной разницы между произвольными действительными числами, стандартной метрики действительных чисел.

Комплексные числа

где х и у являются действительными числами, то абсолютное значение или модуль из г обозначается | z | и определяется

Когда комплексное число z выражается в полярной форме как

Комплексное абсолютное значение разделяет четыре основных свойства, приведенных выше для реального абсолютного значения.

Важно отметить, что свойство субаддитивности (« неравенство треугольника ») распространяется на любой конечный набор из n комплексных чисел как ( z k ) k знак равно 1 п <\ textstyle (z_ ) _ ^ >

Доказательство комплексного неравенства треугольника

Функция абсолютного значения

Связь со знаковой функцией

Функция абсолютного значения действительного числа возвращает его значение независимо от его знака, тогда как функция знака (или знака) возвращает знак числа независимо от его значения. Следующие уравнения показывают взаимосвязь между этими двумя функциями:

Производная

Реальная функция абсолютного значения является примером непрерывной функции, которая достигает глобального минимума там, где производная не существует.

Первообразный

Первообразной (неопределенного интеграла) вещественной функции абсолютного значения

Расстояние

Стандартное евклидово расстояние между двумя точками

Это можно рассматривать как обобщение, поскольку для и реального, то есть в 1-пространстве, согласно альтернативному определению абсолютного значения, а 1 <\ displaystyle a_ <1>> б 1 <\ displaystyle b_ <1>>

Выше показано, что расстояние «абсолютное значение» для действительных и комплексных чисел согласуется со стандартным евклидовым расстоянием, которое они наследуют в результате рассмотрения их как одномерного и двумерного евклидова пространства соответственно.

Свойства абсолютного значения разности двух действительных или комплексных чисел: неотрицательность, тождество неразличимых, симметрия и неравенство треугольника, данные выше, можно рассматривать как мотивирующие более общее понятие функции расстояния следующим образом:

Обобщения

Заказанные кольца

Четыре основных свойства абсолютного значения для действительных чисел могут использоваться для обобщения понятия абсолютного значения на произвольное поле следующим образом.

Векторные пространства

Опять же, фундаментальные свойства абсолютного значения для действительных чисел могут быть использованы, с небольшими изменениями, для обобщения этого понятия на произвольное векторное пространство.

Композиционные алгебры

Источник

Абсолютные и относительные величины

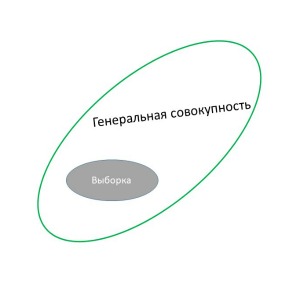
Что представляют собой абсолютные и относительные величины мы скажем немного позже. Для начала поясним про совокупность. Существует генеральная совокупность – это все. Все кто есть номинально. Допустим все женщины, которые живут в городе Москве. Но, мы же не будет опрашивать всех женщин по всей Москве. Нам достаточно, опросить пару десятков, чтобы сделать вывод по всей совокупности (всем).

И вот непосредственно кого мы опрашиваем это и есть выборка.

Выборка должна быть репрезентативной. То есть, соответствовать генеральной совокупности. Если мы исследуем женщин в Москве. Не нужно опрашивать мужчин или жителей другого города.

Теперь, непосредственно, поговорим про величины. Они бывают абсолютные и относительные.

Абсолютные величины — это те, которые есть как есть. Например, количества инвесторов, открывших счета в марте 2020 году на Московской бирже. Данный массив можно назвать генеральной совокупность и обозначить в виде N. А вот каждого инвестора представить, как единицу, числом X. И еще давайте разделим всех инвесторов по группам. Например, как на сайте бирже, по типу клиентов: физлица, юрлица и другие. Группа, в которой есть определенная частота (количественно по определенному признаку), обозначиться это так f(x).

Всего новых 6 919 274, а юридических лиц в количестве 25 524.

Генеральная совокупность, новые клиенты в марте на всей Мосбирже, N = 6 919 274.

Один новый клиент – это X ед.

Из них юридических лиц f(x) = 25 524. То есть, количество клиентов в одной группе.

Кстати, в марте, в разгар пандемии количество новых клиентов физлиц было рекордным, более 6 миллионов.

По сути абсолютные величины — это количество в совокупности или выборки. Число инвесторов, инвесторов, которых мы опросили. Для удобства всех инвесторов можно разделить на группы.

Но, есть еще качественные данные. Допустим, при опросе респонденты указывают свои доходы в рублях, то это количественные данные. А если они сообщают свой пол, возраст, город или ответ в виде да/нет, то это уже качественные показатели.

Переходим к относительным величинам. Здесь все понятно, это значения сравнения с базовыми данными.

Измеряться они уже не штуками, а коэффициентами, процентами и промиллями.

Интенсивные показатели. Отношение явления к среде. Например, количества инвесторов в России к всему населению. Получиться маленькое число умножим его на 100 и будет показатель в виде процентов. Относительные показатели на ваше усмотрение можно домножать на K – кратное 10, 100 и 1000. (Явление/Среда)хK. 2млн/140млн х 100 = 1,42%.

Экстенсивные показатели. Отображают концентрацию (структуру). Например, соотнести тех инвесторов, которые совершают сделки и с теми, кто неактивен. Получим круговую диаграмму и увидим структуру. (Часть совокупность №1/часть совокупность №2)хK.

Соотношение. Тут понятно, совокупность к совокупности. К примеру, сколько выпущено облигации и сколько инвесторов на мосбрже. То есть на сколько инвесторов приходиться количество облигации. Допустим инвесторов 1 млн человек и облигации выпущено 10 млн штук. Вот на каждый инвертор приходится 10 облигаций. (совокупность №1/часть совокупность №2)хK.

Наглядная (показательная) статистика. Для того, чтобы показать динамику. То есть, вот в том то году было так мало, а сейчас много.

Это отношения текущего периода к базовому. (Текущий год/базовый год) х 100%. Например, в 2018 мало инвесторов на бирже, в 2019 стало много. И получим, наверное, 500%, то есть в 5 раз больше стало инвесторов.

Вот так несложно все получается. Абсолютные и относительные величины встречаются в практике постоянно. Если, что-то непонятно, пишите нам.

Источник