что значит стохастический алгоритм

Как изображено на картинке выше, при детерминированном шаге, вычисления происходят как обычно. Однако при подбрасывании монетки вычисление разветвляется. Вместо линейной последовательности получается дерево вычисления. Каждая ветвь этого дерева называется путем вычисления. Путь характеризуется значениями случайных битов. Каждый раз, подбрасывая монетку, мы выбираем одно из двух направлений движения. Таким образом, мы допускаем некоторую вольность: разрешаем, чтобы алгоритм корректно работал не на всех путях, а только на некоторых. Прежде чем переходить к оценке возможностей ошибки вероятностных алгоритмов, оговорим некоторые технические детали.

Во-первых, у подбрасываемой монетки может быть много сторон (исходов). Во-вторых, вероятности выпадения всех возможных исходов не обязательно должны быть равны. Однако сумма всех возможных исходов всегда равна 1.

Подсчет вероятности ошибки

Задача проверки равенства третейским судьей

Рассмотрим задачу с более сложным условием. Алиса знает двоичное слово x длины n. Боб знает слово y той же длины. Они имеют возможность передать Чарли некоторую информацию (слова u и v), по которой Чарли должен решить, равны ли слова x и y. Цель: передать как можно меньше битов при условии, что Чарли правильно отвечает на любых x, y. Алиса с Бобом друг с другом общаться не могут.

Случайность как «канал связи»

Попробуем решить туже задачу, но теперь представим, что Алиса и Боб имеют доступ к общему источнику случайности. Скажем, к одному и тому же изданию книги «Таблица случайных чисел». Цель: передать как можно меньше битов при условии, что вероятность ошибки Чарли мала на любых x, y.

Попробуем решить эту задачу и определить, можно ли таким образом передавать меньше битов, чем с помощью детерминированного алгоритма.

Алиса и Боб выбирают случайное простое число p (одно и то же, случайность общая для них обоих) в интервале от n до 2n.

При наличии общей случайности для любого ε > 0 существует такой способ выбора сообщений, который гарантирует решение задачи равенства с вероятностью ошибки меньше ε и передает O(log n) битов. Запись g (n) = O(f(n)) означает, что есть такие числа C и n₀, что для всех n > n₀ выполняется g(n) 4/5 (примерно 1 − 1/e 2 ). И оказывается, что это почти все, чего мы можем достичь. Рассмотрим частный случай теоремы Бабаи – Киммеля, из которой следует, что при любом способе вероятностного выбора сообщений в задаче равенства, гарантирующем вероятность ошибки меньше 1/3, длина переданных сообщений Ω(√n). Запись g(n) = Ω(f(n)) означает, что есть такие числа C и n₀, что для всех n > n₀ выполняется g(n) > Cf(n).

Посмотрев лекцию до конца, вы узнаете, как благодаря внедрению случайности можно ускорять работу алгоритма, а также о понятии фальшивой случайности.

Источник

4.2.3. Стохастические алгоритмы

Суть стохастического подхода заключается в изменении весовых коэффициентов сети случайным образом и сохранении тех изменений, которые ведут к уменьшению заданной целевой функции. Под целевой функцией в данном случае понимается величина Е(w)_kдля k-го входного образа

. (4.27)

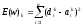
В начале обучения производятся достаточно большие случайные коррекции веса, которые затем постепенно уменьшаются. При этом для исключения «зависания» алгоритма в локальных минимумах должны сохранятся не только те изменения синаптической карты, которые ведут к уменьшению целевой функции, но также изредка и изменения, приводящие к ее увеличению. Такое обучение позволяет сети, в конце концов, стабилизироваться в близи глобального минимума.

Стратегия изменения синаптической карты строится на аналогии с физическими процессами, происходящими при отжиге металла. В расплавленном металле атомы находятся в беспорядочном движении. При понижении температуры атомы стремятся к состоянию энергетического минимума (кристаллизации), т.е., к глобальному минимуму.

Энергетическое состояние НС описывается распределением Больцмана

, (4.28)

где P(E) – плотность распределения энергии сети Е (вероятность того, что система находится в состоянии с энергией Е); k – постоянная Больцмана (выбирается в зависимости от задачи); Т – искусственная температура.

4.2.3.1. Машина Больцмана

Нейронная сеть называется машиной Больцмана, если она основана на принципах стохастического обучения и скорость изменения искусственной температуры обратно пропорциональна логарифму времени

, (4.29)

где T(t)– искусственная температура на шагеtалгоритма;Т₀– начальная температура.

Величина случайного шага для машины Больцмана задается распределением Гаусса

, (4.30)

где Р(с)– плотность распределения вероятности величины шагас(вероятность изменения веса на величинус);Т– искусственная температура.

Машина Больцмана характеризуется очень большим временем обучения.

В стохастических алгоритмах случайные изменения могут проводиться:

1) для отдельных весов;

2) всех нейронов слоя в многослойных сетях;

3) для всех нейронов сети одновременно.

Эти модификации алгоритма дают возможность сократить общее число итераций обучения.

4.2.3.2. Машина Коши

Разработан метод быстрого обучения НС стохастическими алгоритмами, основанный на машине Больцмана. В данном методе при вычислении величины шага распределение Гаусса заменяется на распределение Коши

. (4.32)

Распределение Коши имеет, как показано на рис. 4.14, более длинные «хвосты», увеличивая тем самым вероятность больших шагов. С помощью такого простого изменения максимальная скорость уменьшения температуры становится обратно пропорциональной линейной величине, а не логарифму, как для алгоритма обучения Больцмана

. (4.33)

В данном методе можно не только вычислить вероятность изменения веса Р(с), но и явно задать само приращение веса (шаг 4)

, (4.34)

где – дополнительный коэффициент скорости обучения.

Значение шага обучения св данном случае вычисляется методом Монте-Карло. На интервале (–/2,/2) (необходимо ограничить функцию тангенса) в соответствии с равномерным законом распределения выбирается случайное числос. Оно подставляется в формулу (4.34) в качестве Р(с), и с помощью текущей температуры вычисляется величина шага.

Источник

Документация

Стохастические решатели

Когда использовать стохастические решатели

Стохастические алгоритмы симуляции предоставляют практический метод для симуляции реакций, которые являются стохастическими по своей природе. Модели с небольшим количеством молекул могут реалистично быть симулированы стохастическим образом, то есть, позволив результатам содержать элемент вероятности, в отличие от детерминированного решения.

Необходимые условия модели для симуляции со стохастическим решателем

Необходимые условия модели включают:

Если ваша модель содержит события, можно симулировать использование стохастического ssa решатель. Другие стохастические решатели не поддерживают события.

Ваша модель не должна содержать дозы. Никакие стохастические решатели не поддерживают дозы.

Кроме того, если вы выполняете индивидуума или население, соответствующее на модели чей Configset object задает стохастический решатель и опции, иметь в виду это во время подходящего SimBiology ® временно изменения:

SolverType свойство к решателю по умолчанию ode15s

SolverOptions свойство к опциям в последний раз сконфигурировано для детерминированного решателя

Что происходит во время стохастической симуляции?

Во время стохастической симуляции модели программное обеспечение игнорирует любой уровень, присвоение или алгебраические правила если существующий в модели. В зависимости от модели стохастические симуляции могут потребовать большего количества времени вычисления, чем детерминированные симуляции.

Совет

При симуляции модели с помощью стохастического решателя можно увеличить LogDecimation свойство configset object записать меньше точек данных и уменьшить время выполнения.

Стохастический алгоритм симуляции (SSA)

Химическое основное уравнение (CME) описывает динамику химической системы в терминах эволюции времени вероятностных распределений. Непосредственно решение для этого распределения непрактично для большинства реалистических проблем. Стохастический алгоритм симуляции (SSA) вместо этого эффективно генерирует отдельные симуляции, которые сопоставимы с CME путем симуляции каждой реакции с помощью ее функции склонности. Таким образом анализ нескольких стохастических симуляций, чтобы определить вероятностное распределение более эффективен, чем прямое решение CME.

Этот алгоритм точен.

Поскольку этот алгоритм оценивает одну реакцию за один раз, это может быть слишком медленно для моделей с большим количеством реакций.

Если количество молекул каких-либо реагентов огромно, может требоваться много времени, чтобы завершить симуляцию.

Явный Tau-прыгающий алгоритм

Поскольку стохастический алгоритм симуляции может быть слишком медленным для многих практических проблем, этот алгоритм был спроектирован, чтобы ускорить симуляцию за счет некоторой точности. Алгоритм обрабатывает каждую реакцию, как являющуюся независимым от других. Это автоматически выбирает временной интервал, таким образом, что относительное изменение в функции склонности для каждой реакции меньше вашего ошибочного допуска. После выбора временного интервала алгоритм вычисляет число раз, каждая реакция происходит во время временного интервала и делает соответствующие изменения в концентрацию различных химических разновидностей включенными.

Этот алгоритм может быть порядками величины быстрее, чем SSA.

Можно использовать этот алгоритм для больших проблем (если проблема не численно жестка).

Этот алгоритм жертвует некоторой точностью за скорость.

Этот алгоритм не хорош для жестких моделей.

Необходимо задать ошибочный допуск так, чтобы получившиеся временные шаги имели порядок самого быстрого масштаба времени.

Неявный Tau-прыгающий алгоритм

Как явный tau-прыгающий алгоритм, неявный tau-прыгающий алгоритм является также приближенным методом симуляции, спроектированной, чтобы ускорить симуляцию за счет некоторой точности. Это может решить численно жесткие проблемы лучше, чем явный tau-прыгающий алгоритм. Для детерминированных систем проблема, как говорят, численно жестка, если существуют “быстрые” и “медленные” масштабы времени, существующие в системе. Для таких проблем явный tau-прыгающий метод выполняет хорошо, только если он продолжает брать маленькие временные шаги, которые имеют порядок самого быстрого масштаба времени. Неявный tau-прыгающий метод может потенциально сделать намного большие шаги и все еще быть устойчивым. Алгоритм обрабатывает каждую реакцию, как являющуюся независимым от других. Это автоматически выбирает временной интервал, таким образом, что относительное изменение в функции склонности для каждой реакции меньше заданного пользователями ошибочного допуска. После выбора временного интервала алгоритм вычисляет число раз, каждая реакция происходит во время временного интервала и делает соответствующие изменения в концентрацию различных химических разновидностей включенными.

Этот алгоритм может быть намного быстрее, чем SSA. Это также обычно быстрее, чем явный tau-прыгающий алгоритм.

Можно использовать этот алгоритм для больших проблем и также для численно жестких проблем.

Общее количество делаемых шагов обычно меньше explicit-tau-leaping алгоритма.

Этот алгоритм жертвует некоторой точностью за скорость.

Существует более высокая вычислительная нагрузка для каждого шага по сравнению с явным tau-прыгающим алгоритмом. Это приводит к большему процессорному времени на шаг.

Этот метод часто ослабляет возмущения медленного продвижения коллектора к уменьшаемому отклонению состояния о среднем значении.

Ссылки

[1] Гибсон М.А., Брук J. (2000), “Точная стохастическая симуляция химических систем со многими разновидностями и многими каналами”, журнал физической химии, 105:1876–1899.

[2] Гиллеспи Д. (1977), “Точная стохастическая симуляция двойных химических реакций”, журнал физической химии, 81 (25): 2340–2361.

[3] Гиллеспи Д. (2000), “химическое уравнение Langevin”, журнал химической физики, 113 (1): 297–306.

[4] Гиллеспи Д. (2001), “Аппроксимированная ускоренная стохастическая симуляция химически реагирующих систем”, журнал химической физики, 115 (4):1716–1733.

[5] Гиллеспи Д., Пецолд Л. (2004), “Улучшенный выбор размера прыжка для ускоренной стохастической симуляции”, журнал химической физики, 119:8229–8234

[6] Рэзинэм М., Пецолд Л., Као И., Гиллеспи Д. (2003), “Жесткость в стохастических химически реагирующих системах: неявный Tau-прыгающий метод”, журнал химической физики, 119 (24):12784–12794.

[7] Moler, C. (2003), “Жесткость жестких дифференциальных уравнений является тонкой, трудной, и важной концепцией в числовом решении обыкновенных дифференциальных уравнений”, MATLAB News & Notes.

Источник

стохастический алгоритм

Смотреть что такое «стохастический алгоритм» в других словарях:

Алгоритм муравейника — Поведение муравьёв явилось вдохновением для создания мета эвристической технологии оптимизации Алгоритм муравейника (англ. Ant colony optimization algorithm или ACO) является вероятностной техникой для решения вычислительных задач, которая… … Википедия

Алгоритм — У этого термина существуют и другие значения, см. Алгоритм (значения). Для улучшения этой статьи желательно?: Переработать оформление в соответствии с правил … Википедия

СТОХАСТИЧЕСКИЙ ВЫЧИСЛИТЕЛЬНЫЙАЛГОРИТМ — вычислительный алгоритм, включающий операции со случайными числами, вследствие чего результат вычисления является случайным. Стохастическими являются алгоритмы статистического моделирования, используемые для численного исследования случайных… … Математическая энциклопедия

АЛГОРИТМ ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА-ОПЕРАТОРА — логическая организация деятельности человека оператора, состоящая из совокупности действий и оперативных единиц информации. Использование А. д. ч. о. в инженернопсихологическом проектировании повышает надежность проектирования, снижает затраты,… … Энциклопедический словарь по психологии и педагогике

Муравьиный алгоритм — Поведение муравьёв явилось вдохновением для создания метаэвристической технологии оптимизации Муравьиный алгоритм (алгоритм оптимизации подражанием муравьиной колонии, англ. ant colony optimization, ACO) од … Википедия

Метод Монте-Карло — У этого термина существуют и другие значения, см. Монте Карло (значения). Метод Монте Карло (методы Монте Карло, ММК) общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного)… … Википедия

Монте-Карло (метод) — Метод Монте Карло (методы Монте Карло, ММК) общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные… … Википедия

Монте-Карло метод — Метод Монте Карло (методы Монте Карло, ММК) общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные… … Википедия

Численное интегрирование — (историческое название: (численная) квадратура) вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла. Численное… … Википедия

Стохастичность — (др. греч. στόχος цель, предположение) означает случайность. Стохастический процесс это процесс, поведение которого не является детерминированным, и последующее состояние такой системы описывается как величинами, которые могут быть предсказаны,… … Википедия

Метод обратного распространения ошибки — (англ. backpropagation) метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. А.И. Галушкиным[1], а также независимо и одновременно Полом Дж. Вербосом[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж … Википедия

Источник